Livressur objet Banque de photographies et d’images à haute résolution

Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . YS, qual farà dalle duefùperfìcie FG, GH ailaparte I, M,& così feguendo dvnain vna,comefi ricerca. Venedo dùque allatto della diuizione dellailuione, ballerà prima trouar li tre pùti a b e nella linea <*, li quali li trouano(com edetto nel primo caiojcon numeri perla rtotitia dele frOnti,& della li-nea -, antil tri Fraliti en chordici. Nondimensionnofupponeremo il medefimo di detto primo cafo, che la fronte A BdiLutjofia 24, BC diTitio 15-, CD Banque D'Images

RM2AN3918–Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . YS, qual farà dalle duefùperfìcie FG, GH ailaparte I, M,& così feguendo dvnain vna,comefi ricerca. Venedo dùque allatto della diuizione dellailuione, ballerà prima trouar li tre pùti a b e nella linea <*, li quali li trouano(com edetto nel primo caiojcon numeri perla rtotitia dele frOnti,& della li-nea -, antil tri Fraliti en chordici. Nondimensionnofupponeremo il medefimo di detto primo cafo, che la fronte A BdiLutjofia 24, BC diTitio 15-, CD

Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . ^t DELLE ALLVVIONr. nionnoiìra operando, checonofciutigli inconuenienti di quel-li, e di queilo,locchio infìeme col giudicio Apferoui il cerzo modo. PRIMO ESSEMPIO DELLA DIVIISIONEDEGLI AGRIMENSORI. Ci vede^dalprefente dif-fègno, cheTheofra -ilo , Ari-luppo, Argo, Theo-filo, Me-uio, han-no le portioni loromaggiori,che noncomportala propor-tione delelelor fronti.Geroaftrothia.ETI ha non, efgggggggggalio, no Banque D'Images

RM2AN4GG2–Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . ^t DELLE ALLVVIONr. nionnoiìra operando, checonofciutigli inconuenienti di quel-li, e di queilo,locchio infìeme col giudicio Apferoui il cerzo modo. PRIMO ESSEMPIO DELLA DIVIISIONEDEGLI AGRIMENSORI. Ci vede^dalprefente dif-fègno, cheTheofra -ilo , Ari-luppo, Argo, Theo-filo, Me-uio, han-no le portioni loromaggiori,che noncomportala propor-tione delelelor fronti.Geroaftrothia.ETI ha non, efgggggggggalio, no

Modo del Diferensori diversoMostrato con ragioni mathématiche & con pratica . ifcanoin diuerb punti, due linee rette vguali i due ne iefime, perla fet-nma propofìtione de! Primo dEuclide, perche hauemo dalla me--delìrna linea L O tirati da i punti diuerfi O, & R le due linee O INF,.tkRX, congiunte nei punto N,è imponibile, chelleno fìanoi vguali. Duo altri ineonenienti nafeono , e {Tendo la linea L R-l vgualef lj , luno è, ci l ii contenuto farà vguale al continen- • 1 re, & lalálo, : ù minore fartro à vguale ai, perche Tango-.i lo Banque D'Images

RM2AN341X–Modo del Diferensori diversoMostrato con ragioni mathématiche & con pratica . ifcanoin diuerb punti, due linee rette vguali i due ne iefime, perla fet-nma propofìtione de! Primo dEuclide, perche hauemo dalla me--delìrna linea L O tirati da i punti diuerfi O, & R le due linee O INF,.tkRX, congiunte nei punto N,è imponibile, chelleno fìanoi vguali. Duo altri ineonenienti nafeono , e {Tendo la linea L R-l vgualef lj , luno è, ci l ii contenuto farà vguale al continen- • 1 re, & lalálo, : ù minore fartro à vguale ai, perche Tango-.i lo

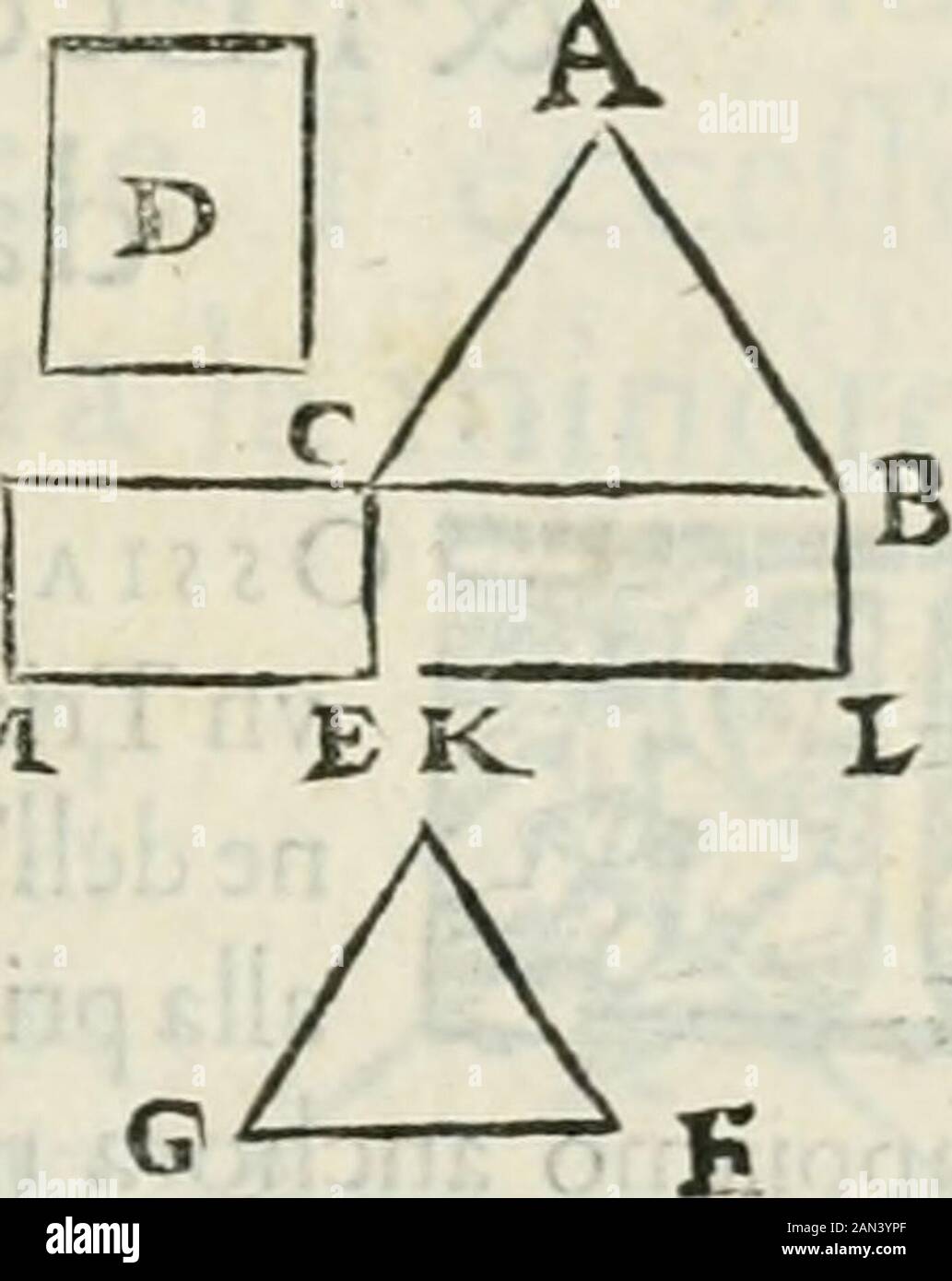
$Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . K L,{àri la F D vguale alla Dj^K Fi ma la F D è vguale Alia : Dunque la F K è vguale alla mede-fima A -, di più,(e G è centro del cerchio L K E, (ara la G E vgualealla G K : Ma la G E è vguale alla C, dunque G K è vguale alla C.la F G fu fatta vguale alla B però le tre linrette K F, F G, & GK fono vguali alle tre A, B, & C. Onde viene consteltituito il trian-golo F G K li Come bibognaua. I I. Datavna linea retta, 5 c vn punto dato Xì^Tuin quella, pofsiamo confci Banque D'Images$

RM2AN48Y0–Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . K L,{àri la F D vguale alla Dj^K Fi ma la F D è vguale Alia : Dunque la F K è vguale alla mede-fima A -, di più,(e G è centro del cerchio L K E, (ara la G E vgualealla G K : Ma la G E è vguale alla C, dunque G K è vguale alla C.la F G fu fatta vguale alla B però le tre linrette K F, F G, & GK fono vguali alle tre A, B, & C. Onde viene consteltituito il trian-golo F G K li Come bibognaua. I I. Datavna linea retta, 5 c vn punto dato Xì^Tuin quella, pofsiamo confci

Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . Modo DEL DIVIDERE LALLVVIONI DA Q.VELLO DI BARTOLO, et DA GLI AGRIMENSORI DIVERSO, Dì Carlo Carra^Zji, detto il Cremona.TRATTATO PRIMO. Deirintentione dellAutore nel trattare delle alluuioni. Bouchon. Primo... Intention mia è di mortrarevnmodoconueniente di diuidere quel terreno, chac-crefciuto da i fiumi, vien detto Alluioneia fin che ciascuno de giintereflàti nella det-ta diuifìone habbia ii fuo ata-propormente, faecondo la larghezza futerolo del fronegata Banque D'Images

RM2AN4HJD–Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . Modo DEL DIVIDERE LALLVVIONI DA Q.VELLO DI BARTOLO, et DA GLI AGRIMENSORI DIVERSO, Dì Carlo Carra^Zji, detto il Cremona.TRATTATO PRIMO. Deirintentione dellAutore nel trattare delle alluuioni. Bouchon. Primo... Intention mia è di mortrarevnmodoconueniente di diuidere quel terreno, chac-crefciuto da i fiumi, vien detto Alluioneia fin che ciascuno de giintereflàti nella det-ta diuifìone habbia ii fuo ata-propormente, faecondo la larghezza futerolo del fronegata

Modo del Dienstódica da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pratica . oi paffare à un cafo di noue mûr, Come quello,che contiene tutte laoperi Geometriche , econengoinogni cafo di cafo di qualfìuoglia al luione di . Dans ta nto auertiamo -, che, al-luionedvna fol ripa, fi domandarà quella; che non lìa angolofa,& quella lì domandarà di due mûre, la quale ha due regolate mûr, che fanno vnangolo, & fuccelsiamente amente laruella larolare di duanno, otto perroli, none, none Banque D'Images

RM2AN3HK7–Modo del Dienstódica da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pratica . oi paffare à un cafo di noue mûr, Come quello,che contiene tutte laoperi Geometriche , econengoinogni cafo di cafo di qualfìuoglia al luione di . Dans ta nto auertiamo -, che, al-luionedvna fol ripa, fi domandarà quella; che non lìa angolofa,& quella lì domandarà di due mûre, la quale ha due regolate mûr, che fanno vnangolo, & fuccelsiamente amente laruella larolare di duanno, otto perroli, none, none

Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . De duo cafi de pritica;Cap. XIII Armi hauerdimotìrato a baldanza di (òpra ilrto-do,comc Ci polTa diuidere qualfìuoglia calò dalluuione propolto, & mafsime per quelli, che mediocrj JPmente hauranno apprelà quella noilra Inllitutione,&hauranno qualche pratica de mifurteri. Nonnetico,tauendoio promellb nel primo Trattato molirare vn modo pra-ticamente , il quale farà nedue fèguenri Cali, con gli eflempijdel quale, fi potrà prédere regrole negli altri : onde g Banque D'Images

RM2AN2NA0–Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . De duo cafi de pritica;Cap. XIII Armi hauerdimotìrato a baldanza di (òpra ilrto-do,comc Ci polTa diuidere qualfìuoglia calò dalluuione propolto, & mafsime per quelli, che mediocrj JPmente hauranno apprelà quella noilra Inllitutione,&hauranno qualche pratica de mifurteri. Nonnetico,tauendoio promellb nel primo Trattato molirare vn modo pra-ticamente , il quale farà nedue fèguenri Cali, con gli eflempijdel quale, fi potrà prédere regrole negli altri : onde g

Modo del Diere l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . ionale. Dooi taglili la C M del-la B C vgualealla I, &: Dal punto M finalmente tirili la M L equi-diitante alla A B . DICO la figura quadrangola ABML elferevguale al retilineo D : percioche la proportion del triangolo AB C, al triangolo CML (PER il x Cap. Del terzo Trattato ) è co mela propore della B C alla C M duplicata, E poiché la procor-tione de i triangoli è Come quella de i lati duplicata, feguitarà, chela proprtione del triangolo A B C al triangolo C Banque D'Images

RM2AN3X2W–Modo del Diere l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . ionale. Dooi taglili la C M del-la B C vgualealla I, &: Dal punto M finalmente tirili la M L equi-diitante alla A B . DICO la figura quadrangola ABML elferevguale al retilineo D : percioche la proportion del triangolo AB C, al triangolo CML (PER il x Cap. Del terzo Trattato ) è co mela propore della B C alla C M duplicata, E poiché la procor-tione de i triangoli è Come quella de i lati duplicata, feguitarà, chela proprtione del triangolo A B C al triangolo C

Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . .à 8: Dal che fi vede, che dieci(àranno le fpecie fpecialifsime della propore justification con ine-gualità-, Cinque appartaenti alla inegualità maggiore,& altre cin-que alla inegualità minore., Alcuno potbe dire, haeguonoi in òtto & non multi-plice;poiche la multiplice è rtata da noi partita in compoJla,& in in-comporta, doueuamoanchoanchor partire la non multiplice iricomporta, & in incompofta: Noncoteo chi con-fider Banque D'Images

RM2AN448X–Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . .à 8: Dal che fi vede, che dieci(àranno le fpecie fpecialifsime della propore justification con ine-gualità-, Cinque appartaenti alla inegualità maggiore,& altre cin-que alla inegualità minore., Alcuno potbe dire, haeguonoi in òtto & non multi-plice;poiche la multiplice è rtata da noi partita in compoJla,& in in-comporta, doueuamoanchoanchor partire la non multiplice iricomporta, & in incompofta: Noncoteo chi con-fider

Modo del Dienstleistódica da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pratica . on 3515VI pro-durrò 5.9670 (ara vguale à quello , che fi farà mulriplicando3978, faconda del faecondo Orcon 15-, ^616, 616, 616 et 616 (ara vgua-le a quel lo, che fi farà mulriplicando 18 con 37 5- 7. Onde talepropore hanno le fronti lVna con laltra, quale hanno le por-tioni lvna con laltra. Par legnare hora le linee diuetoid,è necef-fano prolongare la fronte inchinata,alla linea *,& la linea D ACB,(en tan Banque D'Images

RM2AN2M18–Modo del Dienstleistódica da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pratica . on 3515VI pro-durrò 5.9670 (ara vguale à quello , che fi farà mulriplicando3978, faconda del faecondo Orcon 15-, ^616, 616, 616 et 616 (ara vgua-le a quel lo, che fi farà mulriplicando 18 con 37 5- 7. Onde talepropore hanno le fronti lVna con laltra, quale hanno le por-tioni lvna con laltra. Par legnare hora le linee diuetoid,è necef-fano prolongare la fronte inchinata,alla linea *,& la linea D ACB,(en tan

Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . • ;. Banque D'Images

RM2AN2FJJ–Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . • ;.

Modo del Aldere l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pratica . atiAB,BCfafanno così piroporrionafi alli latiEF, F G,che dallvno,&: Dallaltrohabbabino gt, edene, feifódifódifódifódifódifóní, fódifódijní, fódijódijódijódijní, fódijní, fódijódijó Venez dalla F Galla B G, oaéroA B ad F G, così E F ad B C i embicace-ciotheridirvno5, & nellaltro modo 8 3 È tirata dalla fommi-tà alle bafe. Se dalla cima A del triangolo A B^€alla baie B C fia tirata la perpendiculaires, fi dice queita perdicolare eflèrlal-tezza del triangolo ABC. Banque D'Images

RM2AN42M8–Modo del Aldere l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pratica . atiAB,BCfafanno così piroporrionafi alli latiEF, F G,che dallvno,&: Dallaltrohabbabino gt, edene, feifódifódifódifódifódifóní, fódifódijní, fódijódijódijódijní, fódijní, fódijódijó Venez dalla F Galla B G, oaéroA B ad F G, così E F ad B C i embicace-ciotheridirvno5, & nellaltro modo 8 3 È tirata dalla fommi-tà alle bafe. Se dalla cima A del triangolo A B^€alla baie B C fia tirata la perpendiculaires, fi dice queita perdicolare eflèrlal-tezza del triangolo ABC.

Modo del Dienstecar l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pratica . ttilineo (imilead cflb AB C, & vguale al retilineo D, Per la ter-za propolìtione del 7 Cap. Applihili al- £la linea C B il parallélogrammo BLECvguale al rettilineo A B C, & alla C E, nel jj[langolo CEM per la mededma applica hiCi il parallélogrammo EMF vguale alrettilineo D, di moche do nella nelguale, cem (CEM), alrettilineo C-e-e-gololo (c) Fèndo le linee M E , & E L per dritto , & faranno vnalinea loria, Se il lile faranno le due FC, & C B adunque gli ang Banque D'Images

RM2AN3YPF–Modo del Dienstecar l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pratica . ttilineo (imilead cflb AB C, & vguale al retilineo D, Per la ter-za propolìtione del 7 Cap. Applihili al- £la linea C B il parallélogrammo BLECvguale al rettilineo A B C, & alla C E, nel jj[langolo CEM per la mededma applica hiCi il parallélogrammo EMF vguale alrettilineo D, di moche do nella nelguale, cem (CEM), alrettilineo C-e-e-gololo (c) Fèndo le linee M E , & E L per dritto , & faranno vnalinea loria, Se il lile faranno le due FC, & C B adunque gli ang

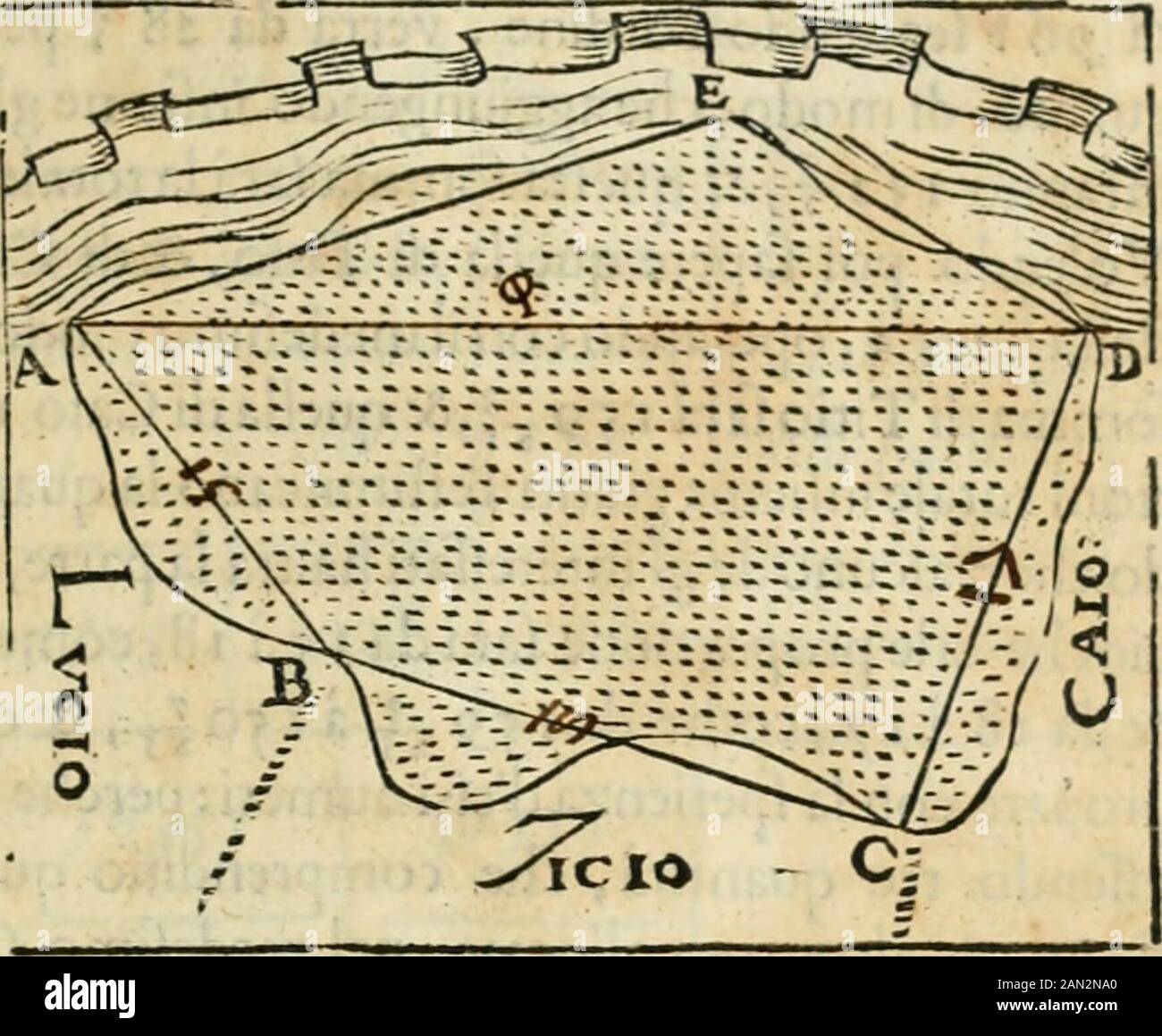
Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . L R ile ò tor J5 TRATTATO QVINTO. LLE,ò tortuofè. Onde di ciò addurre-mo e (Tempio faci-le,ponendo che Dala proporta alluu-uioneABCDEcircondata dalli cantiantiLutio, Ti-tio, & Caio, & daAED verlo il fiu-me, la quète fèn-do irregolata porremo lo (quadronel punel, a & lumili, B & B) (Ara la fronte regolata ài Ludo : poi rimet-tali lo (quadro nel punto B, & guardili C limine di Tino, &: CA-io, & la B C (ar Banque D'Images

RM2AN3KT1–Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . L R ile ò tor J5 TRATTATO QVINTO. LLE,ò tortuofè. Onde di ciò addurre-mo e (Tempio faci-le,ponendo che Dala proporta alluu-uioneABCDEcircondata dalli cantiantiLutio, Ti-tio, & Caio, & daAED verlo il fiu-me, la quète fèn-do irregolata porremo lo (quadronel punel, a & lumili, B & B) (Ara la fronte regolata ài Ludo : poi rimet-tali lo (quadro nel punto B, & guardili C limine di Tino, &: CA-io, & la B C (ar

Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . 5° TRATTATO SECONDO 6. Dignit,Ì.Cap.. Equipements; perche pigliaremo la ci, vguale alla EG, la CLvguale alla EH, & là im vguale al/a GH, dopoi per li centrique, & I, faecondo ginterualli C L, & IM, fi defcriueranno i cer-chi i, cjuil (dunel, K-fánali, K-i & fi farà il triangolo IC K,vguale al triangolo G E H, per laprecedente propofitione. Peròdico, che langolo I C K è vgua-le aliangolo D EF; percioche lidue lati ci, C K, fono vguali allidue lati G E, E H, & lvn Banque D'Images

RM2AN48BC–Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . 5° TRATTATO SECONDO 6. Dignit,Ì.Cap.. Equipements; perche pigliaremo la ci, vguale alla EG, la CLvguale alla EH, & là im vguale al/a GH, dopoi per li centrique, & I, faecondo ginterualli C L, & IM, fi defcriueranno i cer-chi i, cjuil (dunel, K-fánali, K-i & fi farà il triangolo IC K,vguale al triangolo G E H, per laprecedente propofitione. Peròdico, che langolo I C K è vgua-le aliangolo D EF; percioche lidue lati ci, C K, fono vguali allidue lati G E, E H, & lvn

Modo del Dizagensori diversMostrato con ragioni mathématiche & con pratica . diuidendoil quadrato di 8. Men rad.40. En due parti tali,che olferuino la pro-portione da 5 à 1, quella fée à menautrauere 54. 11 5.7. I,& la rad. Vniuerfàledi quello è 54 f men rad. Iyj-j& tale farà la dillanza dal punto A al punto R, & per fàpère an-chora il punto Qj diuidiili il quadrato di A C in due parti, chab-bino la detta e sproportion5, Il che farà 1 2, Saperla rad. 12.fègnili lontano il punto Q^dal punto A. Onde potrà fecondol Banque D'Images

RM2AN39XR–Modo del Dizagensori diversMostrato con ragioni mathématiche & con pratica . diuidendoil quadrato di 8. Men rad.40. En due parti tali,che olferuino la pro-portione da 5 à 1, quella fée à menautrauere 54. 11 5.7. I,& la rad. Vniuerfàledi quello è 54 f men rad. Iyj-j& tale farà la dillanza dal punto A al punto R, & per fàpère an-chora il punto Qj diuidiili il quadrato di A C in due parti, chab-bino la detta e sproportion5, Il che farà 1 2, Saperla rad. 12.fègnili lontano il punto Q^dal punto A. Onde potrà fecondol

Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . H 0 /J#ZV&^ì%&. Banque D'Images

RM2AN2TX9–Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . H 0 /J#ZV&^ì%&.

Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . E R C H E // defiderio difapere e Ã gli Into-nimi naturale, io ho fempre creduto noneffere huomo,chi non de fiderÃ difapere, &perconconfeguente, chi->con ogni fludio non cerca VÃ nciere le difficile , apco-delle co. Ma chi ejfegutfce taldefiderio, fuperando per indÃ¹ fina fta ogni difficile, quello hoben creduto veramente huomo, Sdegno di efere tra gli altriapprefzzato. Per quefo-ho fempre ammirata INV. Eccellflluftrifi. Fin dafuoi primi Banque D'Images

RM2AN4J33–Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . E R C H E // defiderio difapere e Ã gli Into-nimi naturale, io ho fempre creduto noneffere huomo,chi non de fiderÃ difapere, &perconconfeguente, chi->con ogni fludio non cerca VÃ nciere le difficile , apco-delle co. Ma chi ejfegutfce taldefiderio, fuperando per indÃ¹ fina fta ogni difficile, quello hoben creduto veramente huomo, Sdegno di efere tra gli altriapprefzzato. Per quefo-ho fempre ammirata INV. Eccellflluftrifi. Fin dafuoi primi

Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . I - — . Delle Diffinitioni apartenenti alleuioni. L>ap. I. O r a che fiamopreparati di quelle cole Mathematicali, chefono neceflarie al propos-to nóitió, è tempo, che veniamo àdimo-iVràre varij CA(i da diuideril, faecondo , chehahbiamo promeiTb: Ma prima porremoalune cune diurione, dienzione, aria, Dienzione, Diennali, dialone, diennali, dialone, dialone, dialone, dialone, dialone, dialone, dialone, dial E perche Pellènza delle cole, la quale fi ha dalleDiffinitioni deue précède ere ogni altra cogitione, Banque D'Images

RM2AN3PXE–Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . I - — . Delle Diffinitioni apartenenti alleuioni. L>ap. I. O r a che fiamopreparati di quelle cole Mathematicali, chefono neceflarie al propos-to nóitió, è tempo, che veniamo àdimo-iVràre varij CA(i da diuideril, faecondo , chehahbiamo promeiTb: Ma prima porremoalune cune diurione, dienzione, aria, Dienzione, Diennali, dialone, diennali, dialone, dialone, dialone, dialone, dialone, dialone, dialone, dial E perche Pellènza delle cole, la quale fi ha dalleDiffinitioni deue précède ere ogni altra cogitione,

Modo del Diere l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pratica . tra di quellotirifi la P O équidiibnte alla M N, & der triangolo H P O faccialieflamino,con la portio e-, Ma non elTendo vguale operili in quel modo,che tante volte è fiato detto , & fi tirarà finalmente la P Q. «— eq ui- DELLE ALLVVIONL *77 eqaidilUfealIaKMidouecheIafupcrfìcieHIQJ>Of irà vgualealiaporrions E, & là fùpeifìcie QPNK vaeF, fiatrórialla, górielmanní Banque D'Images

RM2AN2X2R–Modo del Diere l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pratica . tra di quellotirifi la P O équidiibnte alla M N, & der triangolo H P O faccialieflamino,con la portio e-, Ma non elTendo vguale operili in quel modo,che tante volte è fiato detto , & fi tirarà finalmente la P Q. «— eq ui- DELLE ALLVVIONL *77 eqaidilUfealIaKMidouecheIafupcrfìcieHIQJ>Of irà vgualealiaporrions E, & là fùpeifìcie QPNK vaeF, fiatrórialla, górielmanní

Modo del Altrito da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pratica . parendoci, che la cognition loro non fi Apparaltroue -, maintorno alle communi, ci baltarà proportionle fimplicmente, comeque, fontolte, fontolte Fiponno apprentissage daaltri,& malìimamenreda Euclide,dal quale pigliaremo leDiffi- :nitioni, le Dimande, le Dignità, & le Propofitioni, porte da noinel preiente fafecondo Trattato. Né paia firano, che, potendonei rimettere ad Euclide la cogitione di quelli principi; voglia-Mo noncodio porle dans l'opéra de la Vieille Banque D'Images

RM2AN4E11–Modo del Altrito da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pratica . parendoci, che la cognition loro non fi Apparaltroue -, maintorno alle communi, ci baltarà proportionle fimplicmente, comeque, fontolte, fontolte Fiponno apprentissage daaltri,& malìimamenreda Euclide,dal quale pigliaremo leDiffi- :nitioni, le Dimande, le Dignità, & le Propofitioni, porte da noinel preiente fafecondo Trattato. Né paia firano, che, potendonei rimettere ad Euclide la cogitione di quelli principi; voglia-Mo noncodio porle dans l'opéra de la Vieille

Modo del Dilile, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . ionalijfèndo dunque dal punto M tirata la M Lequidiilante alla A B, forma il triangolo L M C lile, & fìmil-defro al triangro ABC. Adunque tal proporefarà del triangolo AB Cai triangolo LM C, Come dal quadratoderelitto (òpra della B Cai quadrato di MC, che altro non vuoldre,che la proportion e della BC alaM C fia duplicata-, cioè, co-me quella della B C H -, F eralla E, F. Onde daquello, fi raccoglie, che tutte le figure retilinee Banque D'Images

RM2AN3WYR–Modo del Dilile, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . ionalijfèndo dunque dal punto M tirata la M Lequidiilante alla A B, forma il triangolo L M C lile, & fìmil-defro al triangro ABC. Adunque tal proporefarà del triangolo AB Cai triangolo LM C, Come dal quadratoderelitto (òpra della B Cai quadrato di MC, che altro non vuoldre,che la proportion e della BC alaM C fia duplicata-, cioè, co-me quella della B C H -, F eralla E, F. Onde daquello, fi raccoglie, che tutte le figure retilinee

Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . £2 HC O perfure A no TRATTATO QVARTO perfure A fùperi la fuperficie B nel parallélogramo F G H E , & la proportion del parallélo-grammo C D H E al parallélogrammo C DG F è sì Come dalla H D alla D G, &: La medefìma fard dalla fuperficie A alla fuperficie B. A-i.Dimadadi doncjueperle cote dette habbiamo leccedo,quefto. Che fi troua infra la fuperficie A, & la fuperfi- cie B,viennent bicognaua. Del diminuire, 6 c accrefcere vn Trianolo . Gap , VIIJL §RpÌ@^ E l rettiline Banque D'Images

RM2AN3XHP–Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . £2 HC O perfure A no TRATTATO QVARTO perfure A fùperi la fuperficie B nel parallélogramo F G H E , & la proportion del parallélo-grammo C D H E al parallélogrammo C DG F è sì Come dalla H D alla D G, &: La medefìma fard dalla fuperficie A alla fuperficie B. A-i.Dimadadi doncjueperle cote dette habbiamo leccedo,quefto. Che fi troua infra la fuperficie A, & la fuperfi- cie B,viennent bicognaua. Del diminuire, 6 c accrefcere vn Trianolo . Gap , VIIJL §RpÌ@^ E l rettiline

Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . ?i^g^Ì! Avendo noi intentione di cauare vna pritica, co- .ì£ S^! Foli me riabbiamo detto, la quale Faciliti lationi al-lo Agrimenore mediocremente erusto nelle Ma-thematiche , riabbamo propoito inoltrar il modo , Come G deua trouare la proportione di due piani commenfurabii,ne i Numerla, quale dimoiìaatione ballano, pròpolmoni blano del Vali laltra di làpère la maggior loro commune mifura. PRIMA PROPOSTA Banque D'Images

RM2AN3TA9–Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . ?i^g^Ì! Avendo noi intentione di cauare vna pritica, co- .ì£ S^! Foli me riabbiamo detto, la quale Faciliti lationi al-lo Agrimenore mediocremente erusto nelle Ma-thematiche , riabbamo propoito inoltrar il modo , Come G deua trouare la proportione di due piani commenfurabii,ne i Numerla, quale dimoiìaatione ballano, pròpolmoni blano del Vali laltra di làpère la maggior loro commune mifura. PRIMA PROPOSTA

Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . AR- 66 TRATTATO TERZO. ARBORO DELLA PROPORTIONEGEOMETRICA. Irjustification.écart de Dellaproportione. II. A propore irrifth non Ci può diuidere inpioporrione con vgualità-,perche,fe folle vguale Ja irrationalità fua, non farebbe irrebaridrifth: Eflendo chelvno,e laltro termine fi cóterrebbe per lvnirà Ja què quantite à rebno, polegno. Banque D'Images

RM2AN440J–Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . AR- 66 TRATTATO TERZO. ARBORO DELLA PROPORTIONEGEOMETRICA. Irjustification.écart de Dellaproportione. II. A propore irrifth non Ci può diuidere inpioporrione con vgualità-,perche,fe folle vguale Ja irrationalità fua, non farebbe irrebaridrifth: Eflendo chelvno,e laltro termine fi cóterrebbe per lvnirà Ja què quantite à rebno, polegno.

Modo del Diere l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pratica . uale al paralle-logrammo F E D G, & per coniequenza al triangolo C dato, ilquale ha langolo, valale guallo venir , MFH-B . I Pitagorici diconono, che treccie conuengono a quello Proble-ma , cioè la linea data, il triangolo, & langolo. La linea data èlareezza, ò Iongezza del parallélogrammo , il Triangolo èlofpatio, & langolo ui bibogna : adunque, le noi vorremo applicare al-la data linea retta il parallélogrammo vguale al triangolo porremoper effempio, ch Banque D'Images

RM2AN478R–Modo del Diere l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pratica . uale al paralle-logrammo F E D G, & per coniequenza al triangolo C dato, ilquale ha langolo, valale guallo venir , MFH-B . I Pitagorici diconono, che treccie conuengono a quello Proble-ma , cioè la linea data, il triangolo, & langolo. La linea data èlareezza, ò Iongezza del parallélogrammo , il Triangolo èlofpatio, & langolo ui bibogna : adunque, le noi vorremo applicare al-la data linea retta il parallélogrammo vguale al triangolo porremoper effempio, ch

Modo del Dienstecar l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pratica . e fi farà vna linea fola, con le fióri regolate dellt conrìnanri, Come il Gap. Traile volte per il sur buterreno, Come al calò 2 del 7 Cap. Alle volte per dentro aìlalluuione, Come al. 4 calo del 7 Cap. & al 1 del 1 o-, alle volte per il fiume, & di là da effo, Come al 2 caio deli8 Cap. Alle volte per ialluuione,& perii riu-me,comeai i,& ; cafòdel 7 Cap.&al r,&$ calò dell 8,&alle voite finalméte dietro al fiume,Come nelli cali Cap. IX, XII & xir,& quando più,& qua Banque D'Images

RM2AN3M9J–Modo del Dienstecar l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pratica . e fi farà vna linea fola, con le fióri regolate dellt conrìnanri, Come il Gap. Traile volte per il sur buterreno, Come al calò 2 del 7 Cap. Alle volte per dentro aìlalluuione, Come al. 4 calo del 7 Cap. & al 1 del 1 o-, alle volte per il fiume, & di là da effo, Come al 2 caio deli8 Cap. Alle volte per ialluuione,& perii riu-me,comeai i,& ; cafòdel 7 Cap.&al r,&$ calò dell 8,&alle voite finalméte dietro al fiume,Come nelli cali Cap. IX, XII & xir,& quando più,& qua

Modo del Diplito con ragioni mathématiche & con pratica . prolpolitione x del primo Lipo ??, diremo, che fendo il parallélogrammo A BC D, legato dal diametro B, & comto al, G-atril, G-D, G-atro, G-atro, G-atro, G, G, G, G Talmente che fi tocchino nelpunto G, li due, che non fono legati dal diametro B D, (1 doman-duno dunque li fupplementi,gh altri rimanenti HF, IE,fidico-no ilare attorno al diametro. ». XXXII. Je Tutte laltre figurerettilinee, (ì chia-mano Trapezie,. Delie Dimande.Gap. IL DIMANDA PRIMA. Je addinlanda daqu Banque D'Images

RM2AN4CCR–Modo del Diplito con ragioni mathématiche & con pratica . prolpolitione x del primo Lipo ??, diremo, che fendo il parallélogrammo A BC D, legato dal diametro B, & comto al, G-atril, G-D, G-atro, G-atro, G-atro, G, G, G, G Talmente che fi tocchino nelpunto G, li due, che non fono legati dal diametro B D, (1 doman-duno dunque li fupplementi,gh altri rimanenti HF, IE,fidico-no ilare attorno al diametro. ». XXXII. Je Tutte laltre figurerettilinee, (ì chia-mano Trapezie,. Delie Dimande.Gap. IL DIMANDA PRIMA. Je addinlanda daqu

Modo del Dimathématiche et con pratica. Emo la faeconda dicanda del protrahere le dette linee, elima, e laltra, ci uirà per applica le linee diudeideiitaalla Alluaalla. DIMANDA PRIMA.1 Che fia lecito,dalla mifura già fattadentro delle linee rette, tirate attornoallailuione.per regolarità.,potere,in ricompenia del buon terreno, e del fiu-me nelladiuifìone, detrahefe dall vno,6c aggialglio no degagalgualli, no. Viens (ària Banque D'Images

RM2AN3JBC–Modo del Dimathématiche et con pratica. Emo la faeconda dicanda del protrahere le dette linee, elima, e laltra, ci uirà per applica le linee diudeideiitaalla Alluaalla. DIMANDA PRIMA.1 Che fia lecito,dalla mifura già fattadentro delle linee rette, tirate attornoallailuione.per regolarità.,potere,in ricompenia del buon terreno, e del fiu-me nelladiuifìone, detrahefe dall vno,6c aggialglio no degagalgualli, no. Viens (ària

Modo del Dienstleistós da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pratica . operchio à cóparationede gli altri. Ma quella obiettione, che pare à fauore di BartoIo,ècontra Bartolo iilo nella iùa X11 figura, doue Titio ha egli anelio ra-due mûr nel iùocampo, epuregli ailègna iui Bartolo cosìpoca quantità dadduione, riipetto àgli tri allaperuonde; Poiché, dallhauereiòlamente langolo ininfeco, ouero eilrinieco, naïce tanta diuei fifa ; cheeifèndo langolo intinièco nella X11 figura, Titio non h Banque D'Images

RM2AN4ET8–Modo del Dienstleistós da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pratica . operchio à cóparationede gli altri. Ma quella obiettione, che pare à fauore di BartoIo,ècontra Bartolo iilo nella iùa X11 figura, doue Titio ha egli anelio ra-due mûr nel iùocampo, epuregli ailègna iui Bartolo cosìpoca quantità dadduione, riipetto àgli tri allaperuonde; Poiché, dallhauereiòlamente langolo ininfeco, ouero eilrinieco, naïce tanta diuei fifa ; cheeifèndo langolo intinièco nella X11 figura, Titio non h

Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . SECON- JS TRATTATO PRIMO SECONDO ESSEMPIO DELLADIVISIONE DI BARTOLO.. QVello efTempioèvna figura mula della prima, & feconda, fpecie ; la quale ha molte imperfettioni apparaenti. Per-cioche Getoaitro, Argo, e Titio ottengono molto più di quel-lo , riche erca la ragione, &c Pithia Theofralo, Ariiìippo, Theofilo, Meuio, e Caio non folo non hanno quello, che le gli viene-, ? Ma DELLE ALLVVIONL 1,9 maanchoraibno priuati delladito al fiume, & fi vedechiaramente, che non Banque D'Images

RM2AN4FWG–Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . SECON- JS TRATTATO PRIMO SECONDO ESSEMPIO DELLADIVISIONE DI BARTOLO.. QVello efTempioèvna figura mula della prima, & feconda, fpecie ; la quale ha molte imperfettioni apparaenti. Per-cioche Getoaitro, Argo, e Titio ottengono molto più di quel-lo , riche erca la ragione, &c Pithia Theofralo, Ariiìippo, Theofilo, Meuio, e Caio non folo non hanno quello, che le gli viene-, ? Ma DELLE ALLVVIONL 1,9 maanchoraibno priuati delladito al fiume, & fi vedechiaramente, che non

Modo del Dienstós dell'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pratica . afarmolenza alti a ragione folamente litenza pericon nù-meri,acciò ne venghino chiquelli,che voglione farameno del Agribagno Da noi dunque fi è conchiufo, che la partie di qua della linea $,fèndo 5 84,che le portioni del comparatimétojvna fìa 164$; quel-la di Titio 1 o 27, & di Caio 116j : & le dillanze, che fono da vnpunto altro, oue pafTano le linee diuIDIDO punto Dal pun-to b, rad. F Banque D'Images

RM2AN387R–Modo del Dienstós dell'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pratica . afarmolenza alti a ragione folamente litenza pericon nù-meri,acciò ne venghino chiquelli,che voglione farameno del Agribagno Da noi dunque fi è conchiufo, che la partie di qua della linea $,fèndo 5 84,che le portioni del comparatimétojvna fìa 164$; quel-la di Titio 1 o 27, & di Caio 116j : & le dillanze, che fono da vnpunto altro, oue pafTano le linee diuIDIDO punto Dal pun-to b, rad. F

Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . , faecondo lapropore delle fronti A B, B C, et C D : percioche langolo Aè vguale allangolo H, et il punto Vde rimpetto allo A, è Come ilpunto M de rincontro alla H; Adunque proportale e è dalinea XY Alia &? Quale è dalla NO, alla QJl, et da Ha YZ alla?F Come dalla OP, alla RS: Poiché la proportion del la lineaXYZ,aJla&? È Come quella della linea NO P, alla Qjt Sifèguitarancho che la proportion della Superfìcie A& ? ? allafuperfìcie &??ZYX, farà venir d Banque D'Images

RM2AN3B1X–Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . , faecondo lapropore delle fronti A B, B C, et C D : percioche langolo Aè vguale allangolo H, et il punto Vde rimpetto allo A, è Come ilpunto M de rincontro alla H; Adunque proportale e è dalinea XY Alia &? Quale è dalla NO, alla QJl, et da Ha YZ alla?F Come dalla OP, alla RS: Poiché la proportion del la lineaXYZ,aJla&? È Come quella della linea NO P, alla Qjt Sifèguitarancho che la proportion della Superfìcie A& ? ? allafuperfìcie &??ZYX, farà venir d

Modo del Dienstecar l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pratica . itate Apostolicaexequantur,inuocato eriam ad hoc, fi opus fueiit, auliauxiliaire brachijSasans, contruocato oquistas, fódiliamnódico, fódico, fódico, fódico, fódico, fódico, fódico, fódico, fódico, fódico, fódico, fódico, fódi Se Apoitolica audoritatedeeinimusipiarum praefen-tmm tranfumptis,veIexemplaire isinipio opere imprefsis, plenam ,& eandem prorata fidem, vbiq; tatti in iudicio, quàin extra haberi,qua prasfènrì originali haberetur. Dat. RomsaoudSanóìum Perrum fub Annul Banque D'Images

RM2AN4J66–Modo del Dienstecar l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pratica . itate Apostolicaexequantur,inuocato eriam ad hoc, fi opus fueiit, auliauxiliaire brachijSasans, contruocato oquistas, fódiliamnódico, fódico, fódico, fódico, fódico, fódico, fódico, fódico, fódico, fódico, fódico, fódico, fódi Se Apoitolica audoritatedeeinimusipiarum praefen-tmm tranfumptis,veIexemplaire isinipio opere imprefsis, plenam ,& eandem prorata fidem, vbiq; tatti in iudicio, quàin extra haberi,qua prasfènrì originali haberetur. Dat. RomsaoudSanóìum Perrum fub Annul

Modo del Dienstecar l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pratica . arà legnare la lineammm ddd. Hora volendo loin legnare le lineediuinterdli eee T, kkfff ggg * lì potrà fare Come lì è detto nel terzo Calo del 7. Bouchon. òcon il modo moilrato nel lecondo Calo, ouero con numeri co-me in detto terzo Calo-, per il che lì concluderà, che lallu uione là-1 à.compartita, come eraii bilogno, cioè la lùperfìcie L nn tt ss, diGeroallo, la uu ss tt, Theo-xx, rdjathiq, rdjdjdjdjdjdjdjdjdjdjdjdjdjdjdjdjdjdjdjdj Ia.qq yy P pp > di Ariilippo, la pp P zz 00, Banque D'Images

RM2AN2NN0–Modo del Dienstecar l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pratica . arà legnare la lineammm ddd. Hora volendo loin legnare le lineediuinterdli eee T, kkfff ggg * lì potrà fare Come lì è detto nel terzo Calo del 7. Bouchon. òcon il modo moilrato nel lecondo Calo, ouero con numeri co-me in detto terzo Calo-, per il che lì concluderà, che lallu uione là-1 à.compartita, come eraii bilogno, cioè la lùperfìcie L nn tt ss, diGeroallo, la uu ss tt, Theo-xx, rdjathiq, rdjdjdjdjdjdjdjdjdjdjdjdjdjdjdjdjdjdjdjdj Ia.qq yy P pp > di Ariilippo, la pp P zz 00,

Modo del Coorderer l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pratica . percioche ,{èla proportion della C S Allas R, ècome dalla LP alla PN, perla limitudine delle due figure ABC,& HIL, la L1 Lalla D, RC alla D Venez dalla SUR alla NL. De la portione TRC, fard quella,che conuiene a Titio,&c la ortione A B T R à Lutio, venez bilògnaua. CAFO fecondo di duo encantianti, i qualihanno langolo eftrinfeco al terreno. SIA lalluuione ABCD da diuiderfi tra li duo connati Lutio, & Titio, che hano le fróti AB, & BC regolate, le qua Banque D'Images

RM2AN3EDT–Modo del Coorderer l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pratica . percioche ,{èla proportion della C S Allas R, ècome dalla LP alla PN, perla limitudine delle due figure ABC,& HIL, la L1 Lalla D, RC alla D Venez dalla SUR alla NL. De la portione TRC, fard quella,che conuiene a Titio,&c la ortione A B T R à Lutio, venez bilògnaua. CAFO fecondo di duo encantianti, i qualihanno langolo eftrinfeco al terreno. SIA lalluuione ABCD da diuiderfi tra li duo connati Lutio, & Titio, che hano le fróti AB, & BC regolate, le qua

Modo del Diere l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pratica . di «li yJM: Ascenseur -*• SS! Mi r «il. • ; Banque D'Images

RM2AN2GYC–Modo del Diere l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pratica . di «li yJM: Ascenseur -*• SS! Mi r «il. • ;

Modo del Dienstleza da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pratica . alle date d'échéance lince AB,6 c BC riabbiamotrouata la linea B D mezana proporriónale ??> ilche biìognaua fare. I I. Pofsiamo (opra vna data retta linea de-fcriuere vn rettilineo fimile, òcfimiJ-mcnte pofto ad vno rettilineo dato, Sia la data retta linea A B, & il dato rettilineoC D E F, & bifopra la data retlinta linea A, URIERE, PÒILO riere Venez C D E F, giunghifì la F D, & nelii punti della linea A B connutuiichinfi gli angoli B A Banque D'Images

RM2AN400Y–Modo del Dienstleza da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pratica . alle date d'échéance lince AB,6 c BC riabbiamotrouata la linea B D mezana proporriónale ??> ilche biìognaua fare. I I. Pofsiamo (opra vna data retta linea de-fcriuere vn rettilineo fimile, òcfimiJ-mcnte pofto ad vno rettilineo dato, Sia la data retta linea A B, & il dato rettilineoC D E F, & bifopra la data retlinta linea A, URIERE, PÒILO riere Venez C D E F, giunghifì la F D, & nelii punti della linea A B connutuiichinfi gli angoli B A

Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . C ? TER- 20 TRATTATO PRIMO TERZO ESSEMPIO DELLA DIVI-SIONE PELLAVTORE,. Sendo maniefto quanto habbiamo detto di (opra della proporte, che fi deueoflferuare, e delladito, che fi deuehauere alplume, fi può conokere chiaramente, che tutti gintereflati han-no Tvno, & laltro, fi ponche no contentarli : La cjual colà manife ltamente DELLE ALLVVIONL 2 1 KX// ltamente lì conoscerà dalla dimofiratione di detto caio nel quintoTrattato, al caio XIIII, Habbiamo dunque dim Banque D'Images

RM2AN4EDB–Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . C ? TER- 20 TRATTATO PRIMO TERZO ESSEMPIO DELLA DIVI-SIONE PELLAVTORE,. Sendo maniefto quanto habbiamo detto di (opra della proporte, che fi deueoflferuare, e delladito, che fi deuehauere alplume, fi può conokere chiaramente, che tutti gintereflati han-no Tvno, & laltro, fi ponche no contentarli : La cjual colà manife ltamente DELLE ALLVVIONL 2 1 KX// ltamente lì conoscerà dalla dimofiratione di detto caio nel quintoTrattato, al caio XIIII, Habbiamo dunque dim

Modo del Dienstleistema da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . chilla propohrione Ã¨ il conuerlo della prima di quello ; neci occorre dans quella, Se non compone MD Ghino i- del trpoccino. 2,del Ã³.Cap.diquefto. Tropoft.xo.del 6. C-ipdi tjtiefto.popopofr. Idel 5 . Cap.dicjuclí. Vropuji. Capuchon $.al. 6. Lap ro- i6 TRATTATOa V ARTCT la poportione dimottrato nel XI capo del ? Trattato: De iettantepoi ne fenilica vna jftefi conuenienza i egli Ã¨ ben vero, che da queIh fi comprénde eflTere polsibile di multiphcare qualhuog Banque D'Images

RM2AN3THK–Modo del Dienstleistema da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . chilla propohrione Ã¨ il conuerlo della prima di quello ; neci occorre dans quella, Se non compone MD Ghino i- del trpoccino. 2,del Ã³.Cap.diquefto. Tropoft.xo.del 6. C-ipdi tjtiefto.popopofr. Idel 5 . Cap.dicjuclí. Vropuji. Capuchon $.al. 6. Lap ro- i6 TRATTATOa V ARTCT la poportione dimottrato nel XI capo del ? Trattato: De iettantepoi ne fenilica vna jftefi conuenienza i egli Ã¨ ben vero, che da queIh fi comprénde eflTere polsibile di multiphcare qualhuog

Modo del DienstlegsoMostrato con ragioni mathématiche & con pratica . mp; facciali legnar al folito la Ii-neaN E, la quale mifurata fard pafsi 8. Inoltre mifurifi la linea ODE pafsi i o,& Delle fino nella M pafsi 7,& iui fegnifi M,& nel pùto M fi rimetta lo fqua. Ad angolo retto con la O G, & mirifi F, nella circòferenza, & fegnifi la F, la fafé, la fafsi, è , & min G pasfi 6 .Di rtouo ripoghifi lo (qua. Nel puto G, &c de li (ì tut1A,fègnado ài folirò, ouero facédo legnare la linea retta G A, & inandado verfb A, confid Banque D'Images

RM2AN3NEX–Modo del DienstlegsoMostrato con ragioni mathématiche & con pratica . mp; facciali legnar al folito la Ii-neaN E, la quale mifurata fard pafsi 8. Inoltre mifurifi la linea ODE pafsi i o,& Delle fino nella M pafsi 7,& iui fegnifi M,& nel pùto M fi rimetta lo fqua. Ad angolo retto con la O G, & mirifi F, nella circòferenza, & fegnifi la F, la fafé, la fafsi, è , & min G pasfi 6 .Di rtouo ripoghifi lo (qua. Nel puto G, &c de li (ì tut1A,fègnado ài folirò, ouero facédo legnare la linea retta G A, & inandado verfb A, confid

Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . DELLE ALLVVIONI. 6 t guale ad vn rettileo dato. SIA il dato retilineo A,&bifogni defcriuere vn qua-drato ad EFSA vguale :con-ftituiicalì il parallélogramme-mo rertangoìo BCDE vguale al retilineo A ; ma fèi la-. Q.Tropofit. Co E D (ara vguale al lato B E, shauraà quel lì e, ca q.cap.è cerche E, prolonghilì la B E en F, ponendo E F, vgua-le alla E D, e diuidalì la B F en raison de la Vgnali nel punto G, facen-do centro nel detto punto G, delcr Banque D'Images

RM2AN4521–Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . DELLE ALLVVIONI. 6 t guale ad vn rettileo dato. SIA il dato retilineo A,&bifogni defcriuere vn qua-drato ad EFSA vguale :con-ftituiicalì il parallélogramme-mo rertangoìo BCDE vguale al retilineo A ; ma fèi la-. Q.Tropofit. Co E D (ara vguale al lato B E, shauraà quel lì e, ca q.cap.è cerche E, prolonghilì la B E en F, ponendo E F, vgua-le alla E D, e diuidalì la B F en raison de la Vgnali nel punto G, facen-do centro nel detto punto G, delcr

Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . ÒcEF équidihnti alla BC: DICO, che la linea ABvien legata nelle parti proportionali F, & G. Tropof.del 6. Capo, DEL 2. Trat, N } par 102 TRATTATO QVARTO ;. Tropof.del 4. Cap.deh.T rat. 2. T.1t. Par la précédente propofitione, conte propore è dalla A DallaD C, Come dalla A G, alla G B, & dall A E al- A.la E C,così dalla A F alla F G, tirili anchora la li- ea E K equidiiìante alla A B, Di nouo la prò- ^|t?^portionedella de alla D C (arafi come dalla Q—JATDE H al Banque D'Images

RM2AN41CN–Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . ÒcEF équidihnti alla BC: DICO, che la linea ABvien legata nelle parti proportionali F, & G. Tropof.del 6. Capo, DEL 2. Trat, N } par 102 TRATTATO QVARTO ;. Tropof.del 4. Cap.deh.T rat. 2. T.1t. Par la précédente propofitione, conte propore è dalla A DallaD C, Come dalla A G, alla G B, & dall A E al- A.la E C,così dalla A F alla F G, tirili anchora la li- ea E K equidiiìante alla A B, Di nouo la prò- ^|t?^portionedella de alla D C (arafi come dalla Q—JATDE H al

Modo del Diversito con ragioni mathématiche & con pratica . b •?, perche nel difcorfo, cheriabbifatamo to, nel retilineo lile allo infto, criterios & filimmentepollo,& vguale al parallélogrammo OP,rhauemoritrouato te-re delati equidillantiiperilche gli ballarà collocare lo fquadro nelpunto B cancelo di Lutio,eTitio ad angolo retto con la linea*, &ardardrando verguando verrutino, finternao di Lutino, Tritio di fístino, Itino, Itino, Itino, Itino, Itino, Itino, Itino, Itino, Itino, Itino, Itino, Itino, Itino, Itino, I & mirando verfo il fiume farà legnare la Banque D'Images

RM2AN3HFE–Modo del Diversito con ragioni mathématiche & con pratica . b •?, perche nel difcorfo, cheriabbifatamo to, nel retilineo lile allo infto, criterios & filimmentepollo,& vguale al parallélogrammo OP,rhauemoritrouato te-re delati equidillantiiperilche gli ballarà collocare lo fquadro nelpunto B cancelo di Lutio,eTitio ad angolo retto con la linea*, &ardardrando verguando verrutino, finternao di Lutino, Tritio di fístino, Itino, Itino, Itino, Itino, Itino, Itino, Itino, Itino, Itino, Itino, Itino, Itino, Itino, Itino, I & mirando verfo il fiume farà legnare la

Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . 1 la perpendiculairement NQfopra la LM, la quale diuide il detto rettili-neo nelli duo trianoli LNQ, NQMj dopo leghili dei triangoloLNQ ynafùperficie vgualealla portione H,per la prima propofi-edel.fttimo Capo, La quale farà in quello caio la medesimaN QL vguale alla portione H,& dal triangolo NQM taglili vna fuperfufufufufure vguale alla portione I, co vna linea équidiitante alla NQ, per la medefima propofirionedel fetimo Capo, farfula PO qadpravriciran Banque D'Images

RM2AN3G20–Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . 1 la perpendiculairement NQfopra la LM, la quale diuide il detto rettili-neo nelli duo trianoli LNQ, NQMj dopo leghili dei triangoloLNQ ynafùperficie vgualealla portione H,per la prima propofi-edel.fttimo Capo, La quale farà in quello caio la medesimaN QL vguale alla portione H,& dal triangolo NQM taglili vna fuperfufufufufure vguale alla portione I, co vna linea équidiitante alla NQ, per la medefima propofirionedel fetimo Capo, farfula PO qadpravriciran

Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . TRATTATO HF aVINTO. SRQ.H, alla fuperfìcie PONKI farà venir dalla prima portioneE alla portione G : Onde il retitilinio Hik iarà diuilo halle duelinee QJ^ S, & N O P, Comueniua. VoJendolAgrimèlo.re cocartre lai.luuio-ne ABCci primadiuida langolo C in due parti v-guali con i raggi delloc-chio (ègado la linea <p A Dnel puntoT,etiui fac-cia vn legno - poi per i 1-fe piellie, co-pielli Banque D'Images

RM2AN3BB8–Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . TRATTATO HF aVINTO. SRQ.H, alla fuperfìcie PONKI farà venir dalla prima portioneE alla portione G : Onde il retitilinio Hik iarà diuilo halle duelinee QJ^ S, & N O P, Comueniua. VoJendolAgrimèlo.re cocartre lai.luuio-ne ABCci primadiuida langolo C in due parti v-guali con i raggi delloc-chio (ègado la linea <p A Dnel puntoT,etiui fac-cia vn legno - poi per i 1-fe piellie, co-pielli

Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . V.C i^ /?• -y - ?A-- / Tictp y ra. ^p fia fattoli difTegno, & ineflb fia tirata la linea A D, la quale pafsiper li termini de i canci dellvno, & laltro cancelante ??> & fia an-cho regolata dalle linee AB,BC,DE,& EA, della quale fé ne pigliala mifura, per Iaprima Dimanda, & per la faeconda facciafi il paratelogrammoFG vguale al terreno delalluione.il quale fia poipartito ntre porelle B,CA,CA,CA,CA Banque D'Images

RM2AN3GT2–Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . V.C i^ /?• -y - ?A-- / Tictp y ra. ^p fia fattoli difTegno, & ineflb fia tirata la linea A D, la quale pafsiper li termini de i canci dellvno, & laltro cancelante ??> & fia an-cho regolata dalle linee AB,BC,DE,& EA, della quale fé ne pigliala mifura, per Iaprima Dimanda, & per la faeconda facciafi il paratelogrammoFG vguale al terreno delalluione.il quale fia poipartito ntre porelle B,CA,CA,CA,CA

RM2AN2HJ9–Modo del Diere l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pratica . di «li yJM: Ascenseur -*• SS! Mi r «il

Modo del Alligvioni da qvello di Bartolo, Et de gli agrimensori diversoMostrato con ragioni mathématiche & con pratica . lo delli tre cr)nfinanti,per il ino do deHantecedente,ie ben la fronte AB regolata è minore della fronte BregoIara,peril chepropióga- remo meil de imo/HI punnel to Lintieo, linikle, linikl Che diuidono le pornoni f vna dallaltra faranno la O QJ>, N M, di maniera, che la fuperfìcie HIAQ^P farà vguale alla portione E, & la fu pei fide OQJPMNK. Vguale alla portione F -, & il triangolo M N Lguellio de lingualdo, G. fec Banque D'Images

RM2AN2T5C–Modo del Alligvioni da qvello di Bartolo, Et de gli agrimensori diversoMostrato con ragioni mathématiche & con pratica . lo delli tre cr)nfinanti,per il ino do deHantecedente,ie ben la fronte AB regolata è minore della fronte BregoIara,peril chepropióga- remo meil de imo/HI punnel to Lintieo, linikle, linikl Che diuidono le pornoni f vna dallaltra faranno la O QJ>, N M, di maniera, che la fuperfìcie HIAQ^P farà vguale alla portione E, & la fu pei fide OQJPMNK. Vguale alla portione F -, & il triangolo M N Lguellio de lingualdo, G. fec

Modo del Diere l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pratica . deui compartire fecondo il fòlitomodo sfiammili fé langofo levguale ali angolo K,& la HI alla KL, fé gli, IK-Li angli, Ik & KL fiarco vgualiil retitilineo HIKL farà parallélogrammo, per il primo Cafo del 6. Cap. Ma fé faranno ineguali bifogna-rà dalla parte, oue langolo è maggiore prolongare le due linee IK/& KL fin tanto che le fi congiunghino nel punto M. perilche verràformata vn triangolo cornee HI M, il quale è mezo peroutrarele linfuee, Banque D'Images

RM2AN36H6–Modo del Diere l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pratica . deui compartire fecondo il fòlitomodo sfiammili fé langofo levguale ali angolo K,& la HI alla KL, fé gli, IK-Li angli, Ik & KL fiarco vgualiil retitilineo HIKL farà parallélogrammo, per il primo Cafo del 6. Cap. Ma fé faranno ineguali bifogna-rà dalla parte, oue langolo è maggiore prolongare le due linee IK/& KL fin tanto che le fi congiunghino nel punto M. perilche verràformata vn triangolo cornee HI M, il quale è mezo peroutrarele linfuee,

Modo del Diuilione, 1 fecondi efle-quirla, & gli virimi giudicicarne rettamente ; Ma anchoègioue-uole ad Huo mini di guerra giudiciofìj accioche,oltiail leuar lepianre,pofsino ricono(cere,editribuire qualduoglia fitocamé-te per accmpr Efferati, & ordinar Fortezze . Dunque non (arafuor di propofito inoltrare, Come lì porta fare collo fquadio, chefi adopra nello fquadrare le terrei per elfere ilromenro forfè più fa- Q^ 5 cile ad IG TRATTATO QUINTO Cile viàrIo,& di mino Banque D'Images

RM2AN3P62–Modo del Diuilione, 1 fecondi efle-quirla, & gli virimi giudicicarne rettamente ; Ma anchoègioue-uole ad Huo mini di guerra giudiciofìj accioche,oltiail leuar lepianre,pofsino ricono(cere,editribuire qualduoglia fitocamé-te per accmpr Efferati, & ordinar Fortezze . Dunque non (arafuor di propofito inoltrare, Come lì porta fare collo fquadio, chefi adopra nello fquadrare le terrei per elfere ilromenro forfè più fa- Q^ 5 cile ad IG TRATTATO QUINTO Cile viàrIo,& di mino

Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . H Gpala 7, & mi fi fermi -, perche fi giudica, che il punto G fia derim-petto a langolo E verfò il fiume, & dans elio puntoG ponghiiìlofquadro ad angolo retto con linea , e mirili E, & legnili la lineaGÈ, mifurata pafsi 6, &norifi GD 2; 6; POI parten-doli da Gin andando uerfo F, mifurifì paffì 11 ,che giunti conGH 7, fanne 18, di modo che efTendo FB, HI, paralele, Se vgua-li, la B i farà paralela,& vguale alla HF : dunque la figura rettali-nea CDE ABifcrit Banque D'Images

RM2AN3JWJ–Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . H Gpala 7, & mi fi fermi -, perche fi giudica, che il punto G fia derim-petto a langolo E verfò il fiume, & dans elio puntoG ponghiiìlofquadro ad angolo retto con linea , e mirili E, & legnili la lineaGÈ, mifurata pafsi 6, &norifi GD 2; 6; POI parten-doli da Gin andando uerfo F, mifurifì paffì 11 ,che giunti conGH 7, fanne 18, di modo che efTendo FB, HI, paralele, Se vgua-li, la B i farà paralela,& vguale alla HF : dunque la figura rettali-nea CDE ABifcrit

Modo del Coordere l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pratica . i VX,YX fono fra di loro vguali, dunque il niangolo VXY paragoniti ccn làpdrtionP, & lauanzo, Che fuperala porrione P di e fio triangolò fi rifiruà fin tanto,che fi accrefea iltiiangolo VFY del quadrangolo m VYRvgualea detto auanzo,perla 2. Propofitione del 7. Écart. & il fibile fi faràdaccrefeereil triangolomK-f.de! Quadrando !OTM K& vguale alla PortioneO:Poi il triangolo T& >f, fminuuifchlfi del quadrangolo g T& ivguale alla porrione N, animal de compagnie la prima Propotione Banque D'Images

RM2AN2R4M–Modo del Coordere l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pratica . i VX,YX fono fra di loro vguali, dunque il niangolo VXY paragoniti ccn làpdrtionP, & lauanzo, Che fuperala porrione P di e fio triangolò fi rifiruà fin tanto,che fi accrefea iltiiangolo VFY del quadrangolo m VYRvgualea detto auanzo,perla 2. Propofitione del 7. Écart. & il fibile fi faràdaccrefeereil triangolomK-f.de! Quadrando !OTM K& vguale alla PortioneO:Poi il triangolo T& >f, fminuuifchlfi del quadrangolo g T& ivguale alla porrione N, animal de compagnie la prima Propotione

Modo del Diere l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pratica . HE Ja L è promata vguale alla I,& MNuguale alia CL-, adunque la farà vguale l,ancho putequiallantealanteall. DICO adunque il triangoloABC edere fegato dalla linea M N, così conditamente, che il quadrangolo A B M N, è vguale al retilineo D :percioche , fé la proportion del triangolo MN A B C al quadran-golo ABè (Ì Come dalla E F alla FG,per la cóikuttione-,iarà dalquadrangolo A BMN al triagclo M N C, Come dalla GFalla G E.Inoltre eilendo la M N terme Banque D'Images

RM2AN3WKA–Modo del Diere l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pratica . HE Ja L è promata vguale alla I,& MNuguale alia CL-, adunque la farà vguale l,ancho putequiallantealanteall. DICO adunque il triangoloABC edere fegato dalla linea M N, così conditamente, che il quadrangolo A B M N, è vguale al retilineo D :percioche , fé la proportion del triangolo MN A B C al quadran-golo ABè (Ì Come dalla E F alla FG,per la cóikuttione-,iarà dalquadrangolo A BMN al triagclo M N C, Come dalla GFalla G E.Inoltre eilendo la M N terme

Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . EF G Con il medefimo modo fi può concludere quefto prefente Ca- Z fodelT 178 TRATTATO QVINTO. H 0 /J#ZV&^ì%& Banque D'Images

RM2AN2W5C–Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . EF G Con il medefimo modo fi può concludere quefto prefente Ca- Z fodelT 178 TRATTATO QVINTO. H 0 /J#ZV&^ì%&

Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . I. moAalleilremo D>fi fegna vna linea retta con legni apparaenti,ouero dallo eùremo Dallo ertretimo A delli confinement. Per princi-pio delle opérationi Geodiche è neceffano alla diuizione dellallu-uioni legnare una linea retta co légni apparatti da gli eftremi dogniconfinante uerfo il fiume,afrìnche le linee diutele calchino (opra perpendiculairement,per le ragondo, Fontaiondo. Adducando per eflcrmpiOjche fi come lArchi-tetto n Banque D'Images

RM2AN3MMP–Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . I. moAalleilremo D>fi fegna vna linea retta con legni apparaenti,ouero dallo eùremo Dallo ertretimo A delli confinement. Per princi-pio delle opérationi Geodiche è neceffano alla diuizione dellallu-uioni legnare una linea retta co légni apparatti da gli eftremi dogniconfinante uerfo il fiume,afrìnche le linee diutele calchino (opra perpendiculairement,per le ragondo, Fontaiondo. Adducando per eflcrmpiOjche fi come lArchi-tetto n

Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . R 5 RE due H4 TRATTATO Q.VINTO le due Dimande-Jvna delle quali fìa di mi fu rare terreno dellallu-uione regolata 5 laltra del fare il parallélogrammo, cerne habbiamo detto, il quale fi diuiderà dapoi facondo le proportionli lefronti deconti. ? ; DIMANDA PRIMA. I Che fia lecito mifurare quel fpatiodi terreno 3 detto alluuione, il quale ècomprefo dentro dalle linee rette tira-te intorno ad ella per regolarità. Il conoféere il modo Come fi mifuri il terreno deha Banque D'Images

RM2AN3K93–Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . R 5 RE due H4 TRATTATO Q.VINTO le due Dimande-Jvna delle quali fìa di mi fu rare terreno dellallu-uione regolata 5 laltra del fare il parallélogrammo, cerne habbiamo detto, il quale fi diuiderà dapoi facondo le proportionli lefronti deconti. ? ; DIMANDA PRIMA. I Che fia lecito mifurare quel fpatiodi terreno 3 detto alluuione, il quale ècomprefo dentro dalle linee rette tira-te intorno ad ella per regolarità. Il conoféere il modo Come fi mifuri il terreno deha

Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . endicolor,!! Ha queIlo,chen* cerca, e Come fi troui queitaperpendicolor rilèruiamo ragionarne al primo caio nei fattimoCapo,del quinto trattato ;Oue(i tratta della pritica Agrimenio-ria nella diuifìone dvna Alluione di due mûr. I I I. Ad vna data rettalinea pofsiamo appli 44>*»p°fi 1 rr mone ad prt CARE vn parallélogrammo vguale advn triangolo dato, il qualehabbia vnangolo vguale ad vn angolo dato. SIA la data retta li-nea A, glangolo B,& *?il triangolo C, Banque D'Images

RM2AN47GB–Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . endicolor,!! Ha queIlo,chen* cerca, e Come fi troui queitaperpendicolor rilèruiamo ragionarne al primo caio nei fattimoCapo,del quinto trattato ;Oue(i tratta della pritica Agrimenio-ria nella diuifìone dvna Alluione di due mûr. I I I. Ad vna data rettalinea pofsiamo appli 44>*»p°fi 1 rr mone ad prt CARE vn parallélogrammo vguale advn triangolo dato, il qualehabbia vnangolo vguale ad vn angolo dato. SIA la data retta li-nea A, glangolo B,& *?il triangolo C,

Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . 1 C U £ rà dunque la A,A!IAB la proportion, che hi il numero D, al numero EiPercioche, fendo il piano A al piano B cómenfurabi li, la prò portione 120 TRATTATO QVARTO. Li e r> D portion loro (ara Come danumero à numero , per laquinta propofitione del xdEuclide, ma (è, percafoidetti piani A B foGino quadrati, della IMTA quantità,ilorlati (ariano incomméCurabili, & la loro propor tione nò (Come da da-politionel; Banque D'Images

RM2AN3RNK–Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . 1 C U £ rà dunque la A,A!IAB la proportion, che hi il numero D, al numero EiPercioche, fendo il piano A al piano B cómenfurabi li, la prò portione 120 TRATTATO QVARTO. Li e r> D portion loro (ara Come danumero à numero , per laquinta propofitione del xdEuclide, ma (è, percafoidetti piani A B foGino quadrati, della IMTA quantità,ilorlati (ariano incomméCurabili, & la loro propor tione nò (Come da da-politionel;

$Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pratica . elogrammo E F, & per conlèguenza al rettilineo D . Ondefi G èconitiruitoil retilineo GHK lile al retilineo A B C , Se vguale al retilineo D dato-, ilche fare biiognaua. Del tremare la Quarta proporale , & lEccello di due rettilinei dati. Bouchon. VI H5S3 Ossi amo tre, che nello fminuire, & accrescere^Sj vn Triangolo ma tuttala conclusone della Diuiiìovjj-gEfafl ne dell Alluione-, ma non lì può ciò fare ; {e, (oltraies^si alla prima propofitione del Palato Banque D'Images$

RM2AN3Y7H–Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pratica . elogrammo E F, & per conlèguenza al rettilineo D . Ondefi G èconitiruitoil retilineo GHK lile al retilineo A B C , Se vguale al retilineo D dato-, ilche fare biiognaua. Del tremare la Quarta proporale , & lEccello di due rettilinei dati. Bouchon. VI H5S3 Ossi amo tre, che nello fminuire, & accrescere^Sj vn Triangolo ma tuttala conclusone della Diuiiìovjj-gEfafl ne dell Alluione-, ma non lì può ciò fare ; {e, (oltraies^si alla prima propofitione del Palato

Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . S-Tfosoft-tiene del 5.Cap.dcl 4.Trattato. RA Udo- »*4 TRATTATO QVINTO. RaIelcgiammo H. per la conilruttione ; Il quale e/Tendo vguale aldetto pai alleggiammo ne fegue, che il trapezio M IT K S, faràancho eflb vguale al ogrammo G, Come sì richiede.Onde, voleri*do Agrimenpriderelionelalluionejdiidà primala linea, CA-cundo i c,flegual-fálo, i. Dunque porrà lo (quadro nel Banque D'Images

RM2AN3D43–Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . S-Tfosoft-tiene del 5.Cap.dcl 4.Trattato. RA Udo- »*4 TRATTATO QVINTO. RaIelcgiammo H. per la conilruttione ; Il quale e/Tendo vguale aldetto pai alleggiammo ne fegue, che il trapezio M IT K S, faràancho eflb vguale al ogrammo G, Come sì richiede.Onde, voleri*do Agrimenpriderelionelalluionejdiidà primala linea, CA-cundo i c,flegual-fálo, i. Dunque porrà lo (quadro nel

Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . Sendo maniefto quanto habbiamo detto di (opra della proporte, che fi deueoflferuare, e delladito, che fi deuehauere alplume, fi può conokere chiaramente, che tutti gintereflati han-no Tvno, & laltro, fi ponche no contentarli : La cjual colà manife ltamente DELLE ALLVVIONL 2 1 KX// ltamente lì conoscerà dalla dimofiratione di detto caio nel quintoTrattato, al caio XIIII, Habbiamo dunque dimoltrato le con-dirioni >chedehauuehauereil verdoidere del diuriuriui Banque D'Images

RM2AN4E3H–Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . Sendo maniefto quanto habbiamo detto di (opra della proporte, che fi deueoflferuare, e delladito, che fi deuehauere alplume, fi può conokere chiaramente, che tutti gintereflati han-no Tvno, & laltro, fi ponche no contentarli : La cjual colà manife ltamente DELLE ALLVVIONL 2 1 KX// ltamente lì conoscerà dalla dimofiratione di detto caio nel quintoTrattato, al caio XIIII, Habbiamo dunque dimoltrato le con-dirioni >chedehauuehauereil verdoidere del diuriuriui

Modo del Dienstleza di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . la AH DELLE ALLVVIONT. La A H alla H B, è Ci viennent tous A F alla F G, (ari la proporedella A H H B, Come è dal/a D alla C, i!che bifognaua fare Et fi h.i da fàpère che con quello modo lì può diuidere vna lineain più proporrioni, che ofleruino altrétante proporrioni propo-ne, col congiungerle in(ìeme,comefì vedrà nella fogliente pro-pofìrione. I I I I I. Pofsiamo diriidere vnoParalooram-mo, faecondo più proporrioni date, &con linee équidiitanti .. K D E TG M Banque D'Images

RM2AN4100–Modo del Dienstleza di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . la AH DELLE ALLVVIONT. La A H alla H B, è Ci viennent tous A F alla F G, (ari la proporedella A H H B, Come è dal/a D alla C, i!che bifognaua fare Et fi h.i da fàpère che con quello modo lì può diuidere vna lineain più proporrioni, che ofleruino altrétante proporrioni propo-ne, col congiungerle in(ìeme,comefì vedrà nella fogliente pro-pofìrione. I I I I I. Pofsiamo diriidere vnoParalooram-mo, faecondo più proporrioni date, &con linee équidiitanti .. K D E TG M

Modo del Diere l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pratica . efto per il più tacile, tirandoli dal punto i la im perpendiculairement Hi. , e, le quella diuiderà la HL en due parte vguali, (1 ha-urà queiche li ricerca; Ma, (è farà ineguale, bicognarà far altro difcorfo-, perche trouaremc leccello tra il triangolqjl&il, & il paraiielogrànio F, il quile li ftluaDopoi, per h prima propofìtione del7 Cap.lì fminuiri il riàgolo que IML di tanudialta, tdialta, tdilinialta Banque D'Images

RM2AN3EXT–Modo del Diere l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pratica . efto per il più tacile, tirandoli dal punto i la im perpendiculairement Hi. , e, le quella diuiderà la HL en due parte vguali, (1 ha-urà queiche li ricerca; Ma, (è farà ineguale, bicognarà far altro difcorfo-, perche trouaremc leccello tra il triangolqjl&il, & il paraiielogrànio F, il quile li ftluaDopoi, per h prima propofìtione del7 Cap.lì fminuiri il riàgolo que IML di tanudialta, tdialta, tdilinialta

Modo del Diere l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pratica . s ad altri LE QVATTRO SPECIE dalLVVIONI Proposte da Bartolo nella TlBEfÙA. -»? Delle ALLVVIONr 25 ad altri Filof ori, volle noncotio, par non-tarif ! opera fua rozza,prendere le materie, che per fé faceuano da diuerfi libri rìlofofìci,adornandone i libri f boi. Et noi parimente, par non fare la pré-fente noltra Opera manca,od impermetta habbiamo voluto piglia-re da Euclide i p repèn tip rinci pi ji il che ci pat tanto più lecito,Guanto farà pure dattribuirli a no Banque D'Images

RM2AN4DGA–Modo del Diere l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pratica . s ad altri LE QVATTRO SPECIE dalLVVIONI Proposte da Bartolo nella TlBEfÙA. -»? Delle ALLVVIONr 25 ad altri Filof ori, volle noncotio, par non-tarif ! opera fua rozza,prendere le materie, che per fé faceuano da diuerfi libri rìlofofìci,adornandone i libri f boi. Et noi parimente, par non fare la pré-fente noltra Opera manca,od impermetta habbiamo voluto piglia-re da Euclide i p repèn tip rinci pi ji il che ci pat tanto più lecito,Guanto farà pure dattribuirli a no

Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . r*. H F, G, H, I, faecondo la pròcorrione delie dette quat-tro fronti ;& olrra queftofia fatto il retilineo KLMNO lile allinfcrtoABCDE,6 c vguale alle dettè quartro porrioni,ilqualediuidafl prima dehalluione, acciòche più fi alfaellionamente. Dooi prolunghi fi il lato L M, fin checoncorra nella Ko fibile alla *, nel punto *f» ( perche è inslaataad ella linea Ko ) onde shaurà il triangolo K L .j«, nel quale, per ilprimo Cafo del 8 Banque D'Images

RM2AN2RW5–Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . r*. H F, G, H, I, faecondo la pròcorrione delie dette quat-tro fronti ;& olrra queftofia fatto il retilineo KLMNO lile allinfcrtoABCDE,6 c vguale alle dettè quartro porrioni,ilqualediuidafl prima dehalluione, acciòche più fi alfaellionamente. Dooi prolunghi fi il lato L M, fin checoncorra nella Ko fibile alla *, nel punto *f» ( perche è inslaataad ella linea Ko ) onde shaurà il triangolo K L .j«, nel quale, per ilprimo Cafo del 8

Modo del Diere l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pratica . ione la ragione dellherentia, & dellaprofumiti, mediante la quale Titio ha ragione in quella alluio-ne. Une quefto io potrei rifpondere en due-effet : prima ritorcen-do largomento,& diendo; Se fi due ofleruare la ragione dellad-herentia, e de Ila profumiti, ne feguiranno due inconuenientijilprimo farà, che fpefte volte non sofTeruarà la propore dellefronti de encantianti, onde ciafcuno non hauerà la fua portione fafà, ffafà ffaffafà, ffaffaffaffafà Banque D'Images

RM2AN4GR7–Modo del Diere l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pratica . ione la ragione dellherentia, & dellaprofumiti, mediante la quale Titio ha ragione in quella alluio-ne. Une quefto io potrei rifpondere en due-effet : prima ritorcen-do largomento,& diendo; Se fi due ofleruare la ragione dellad-herentia, e de Ila profumiti, ne feguiranno due inconuenientijilprimo farà, che fpefte volte non sofTeruarà la propore dellefronti de encantianti, onde ciafcuno non hauerà la fua portione fafà, ffafà ffaffafà, ffaffaffaffafà

Modo del Altrevvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pratica . ione VXD alla fuperricie RT-QCVX di Titio farà venir dalla portione G alla portione, &per confèza quènalla fronta, CD. Et fé egli non farà efTercitatoin tali opérationi Aritthmetice,potrà notare vna linea dallangolo A al punto V, Come dalla Halla N, & operare, Come fu detto, nel fecondo Calò del prece-dente Capo, nella linea <p , ne fènút, medefìma diuifìo, debuti-la, debuti-, Banque D'Images

RM2AN39DA–Modo del Altrevvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pratica . ione VXD alla fuperricie RT-QCVX di Titio farà venir dalla portione G alla portione, &per confèza quènalla fronta, CD. Et fé egli non farà efTercitatoin tali opérationi Aritthmetice,potrà notare vna linea dallangolo A al punto V, Come dalla Halla N, & operare, Come fu detto, nel fecondo Calò del prece-dente Capo, nella linea <p , ne fènút, medefìma diuifìo, debuti-la, debuti-,

Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pratica . s^iir-j Twna pròpofìtionc del 6.dEuclide. ^m E ^ue prefètti Dimande non ci feruono ad alrro, che i tf^im à prouarc alcune Propofitioni, che ièguiranno*, ne !.;j !|§&§l ci danno campo di dire altro, (non è che pofsiamo ! IFE^^Mji noi feruircine qua per principi! non dimonurati» ! Poichelle fono Propofitioni prouate da Euclide nel fèifo Balance. DIMANDA PRIMA. J Che i triangoli Se i parallélogrammi,che hanno la medefima altezza, FO-no fra loro , venez le bafe alle baf Banque D'Images

RM2AN42C5–Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pratica . s^iir-j Twna pròpofìtionc del 6.dEuclide. ^m E ^ue prefètti Dimande non ci feruono ad alrro, che i tf^im à prouarc alcune Propofitioni, che ièguiranno*, ne !.;j !|§&§l ci danno campo di dire altro, (non è che pofsiamo ! IFE^^Mji noi feruircine qua per principi! non dimonurati» ! Poichelle fono Propofitioni prouate da Euclide nel fèifo Balance. DIMANDA PRIMA. J Che i triangoli Se i parallélogrammi,che hanno la medefima altezza, FO-no fra loro , venez le bafe alle baf

Modo del Diere l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pratica . ermine mouerfi dvnmoto breiisimo , & vguale, fi formala faconda dimanda, con.fa-cile , & fimpmoïl. Se poi intendiamo la linea retta,termi-narada vna parte, efTereimmobile, e dallaltra mouerfi intor-no al punto, che irà fermo, fi farà la terza dimanda -, percioche ilcentro à faril punto immobile> E linteruallo la linea retta, & E 2 quanto TRATTATO SECONDO quanto ella (èra longa, tanto fefcàfìnterualloà tutte le paia dellacirconferenza. I I I I. Che glang Banque D'Images

RM2AN4BHK–Modo del Diere l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pratica . ermine mouerfi dvnmoto breiisimo , & vguale, fi formala faconda dimanda, con.fa-cile , & fimpmoïl. Se poi intendiamo la linea retta,termi-narada vna parte, efTereimmobile, e dallaltra mouerfi intor-no al punto, che irà fermo, fi farà la terza dimanda -, percioche ilcentro à faril punto immobile> E linteruallo la linea retta, & E 2 quanto TRATTATO SECONDO quanto ella (èra longa, tanto fefcàfìnterualloà tutte le paia dellacirconferenza. I I I I. Che glang

Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . »Xf» dalla parte delira fi paragoni con le due porrionion, & lo eccedo, che auanza delle due porrioni SUR del det-à triangolo *fi X^jfi rifèrua ; Di più fi fminuuifea il triangoloX*f«>f« finiilro della fuperficie i k X «f* vguale allo auanzo rifer-uato. Il che fatto nellangolo i fé constrtitueira la figura quadran-gola nm 1 y vgualla portione P, lile ìkXY lile ralla. Adun-que per tale contiruttione la fuperficie hVki (èra vguale allaportione N, & così faranno rirou Banque D'Images

RM2AN2P7H–Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . »Xf» dalla parte delira fi paragoni con le due porrionion, & lo eccedo, che auanza delle due porrioni SUR del det-à triangolo *fi X^jfi rifèrua ; Di più fi fminuuifea il triangoloX*f«>f« finiilro della fuperficie i k X «f* vguale allo auanzo rifer-uato. Il che fatto nellangolo i fé constrtitueira la figura quadran-gola nm 1 y vgualla portione P, lile ìkXY lile ralla. Adun-que per tale contiruttione la fuperficie hVki (èra vguale allaportione N, & così faranno rirou

Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . 80.88.18. colindri, cilindri. 1 80,88. 30. Propofitione, propofitione, 182. Del7.Cap. 182. 99. 31. A, AB. 183. ipo. 33. AC, AB. 184. iol. I. AC, AB, 185. 101. 5. AB, CA. 187.ioi.io. AC, AB. AC, AB. 104. 1 ». Nel quinto.nelj.Cap.di quello. 189. 1 io. 19- lincna, linea. 195. 129.19-notaries ogni, notaries i canci 198. dogni. jf 198. 134. i.mifurare,mifurarcil. 198.147. IjDC,DC. 17.AB,ab. ALD C,ALDC. I7.C,c. 7, ortione, portione.16. M, MN. 16. la linea, le linee. 1 z. C Banque D'Images

RM2AN2K19–Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . 80.88.18. colindri, cilindri. 1 80,88. 30. Propofitione, propofitione, 182. Del7.Cap. 182. 99. 31. A, AB. 183. ipo. 33. AC, AB. 184. iol. I. AC, AB, 185. 101. 5. AB, CA. 187.ioi.io. AC, AB. AC, AB. 104. 1 ». Nel quinto.nelj.Cap.di quello. 189. 1 io. 19- lincna, linea. 195. 129.19-notaries ogni, notaries i canci 198. dogni. jf 198. 134. i.mifurare,mifurarcil. 198.147. IjDC,DC. 17.AB,ab. ALD C,ALDC. I7.C,c. 7, ortione, portione.16. M, MN. 16. la linea, le linee. 1 z. C

Modo del Dienstleistódico, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pratica . quadrupla fuper fi , farebbe voce improvía luperpartiente-,perche,fè per la prima propofitione dì quollo.4, como apertura e E 70 per j^gf auenimentifàrano 6$t e 14, & quelli làrano li termini radicali di tal propor-tione,& Ci potrà dire efière quadrupla fuper—, la quale nella denatione fuà 4 j. Onde da quello fi potrà raccogliere non ef-fere lecito, propoile che faranno due quantità non pronuntiar Banque D'Images

RM2AN3REH–Modo del Dienstleistódico, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pratica . quadrupla fuper fi , farebbe voce improvía luperpartiente-,perche,fè per la prima propofitione dì quollo.4, como apertura e E 70 per j^gf auenimentifàrano 6$t e 14, & quelli làrano li termini radicali di tal propor-tione,& Ci potrà dire efière quadrupla fuper—, la quale nella denatione fuà 4 j. Onde da quello fi potrà raccogliere non ef-fere lecito, propoile che faranno due quantità non pronuntiar

Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . & qual proporte haueuala prima quantità dell! Angoli aperti alla enze della faecondaquantità delli angoli rebrantti, tal proportione bibgna, che habbiala prima portione di ciafeun encanante alla difieranza della faecon-da portione,elsédo la linea diuidéte ST no toccaua da principiolangolo B, deperalcunco, dopò, depno tocunco, no tocunco, no tocunco, no tocunco, no tocunco, no tocuncunito Che con il rettili-neo HiKL Ci ritroua. Aduque nò fi potrà dar Banque D'Images

RM2AN336A–Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . & qual proporte haueuala prima quantità dell! Angoli aperti alla enze della faecondaquantità delli angoli rebrantti, tal proportione bibgna, che habbiala prima portione di ciafeun encanante alla difieranza della faecon-da portione,elsédo la linea diuidéte ST no toccaua da principiolangolo B, deperalcunco, dopò, depno tocunco, no tocunco, no tocunco, no tocunco, no tocunco, no tocuncunito Che con il rettili-neo HiKL Ci ritroua. Aduque nò fi potrà dar

Modo del Dienstleza di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pratica . iremo, con-forme alla detta 2, propofitione del 7,che iì numero 2 è fa maggiorcommune milùra, che mifuri ambidus i,numero 1, è Per il Corolario della detta 2 propofitione, conciolìa che vnnumero,che mifura dui numeri,mi(ùi aràanchora la loro maggiorcommune milùra: Come (ària, che partendo 24, e io per 2, ne vie1 2,& 5-precifamenre;cioè,l'il maggiore contiene dodici voltela commune milùra, & la minore e vofre Onde è manifeste, cheil numero 2 e l Banque D'Images

RM2AN3T3R–Modo del Dienstleza di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pratica . iremo, con-forme alla detta 2, propofitione del 7,che iì numero 2 è fa maggiorcommune milùra, che mifuri ambidus i,numero 1, è Per il Corolario della detta 2 propofitione, conciolìa che vnnumero,che mifura dui numeri,mi(ùi aràanchora la loro maggiorcommune milùra: Come (ària, che partendo 24, e io per 2, ne vie1 2,& 5-precifamenre;cioè,l'il maggiore contiene dodici voltela commune milùra, & la minore e vofre Onde è manifeste, cheil numero 2 e l

Modo del Dienstleza da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pratica . a linea retta caderà fopra due lineerette, & farà gli angoli alterni vguali, & quelle due linee farannopalele. Di (opra habbiam prounato, che gli angoli NOL,NRLfono bio. Adunque le due linee ON, NR non fono paralle-le y onde, non effendo la linea NR la diuidente, rella che la lineaNO, è la diuidente, & che il retilineo Hik L è diuifò con prohrica. Da quello adunque farà manifeste,fè fi vorrà diriider lalluio-ne che ballata, par le r Banque D'Images

RM2AN33FP–Modo del Dienstleza da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pratica . a linea retta caderà fopra due lineerette, & farà gli angoli alterni vguali, & quelle due linee farannopalele. Di (opra habbiam prounato, che gli angoli NOL,NRLfono bio. Adunque le due linee ON, NR non fono paralle-le y onde, non effendo la linea NR la diuidente, rella che la lineaNO, è la diuidente, & che il retilineo Hik L è diuifò con prohrica. Da quello adunque farà manifeste,fè fi vorrà diriider lalluio-ne che ballata, par le r

Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . : Come i trianoli ABC, & A C D, & i paradiogrammi E C, & dal parallélogrammo E C al Bparallélogrammo C F. I I. I Che qualfiuoglia triangolò fegato convna linea équidiftante à qualfiuoglialato , che i Iati dei famenegto fiano proporalitali . Venez che il triangolo ABC legato dalla li-nea D E equidillante alla B C, la proportio-ne dell A E alla E B Ga, venez dall A D alia D C :& quella è nota, eflendo la feconda propoita di-mollrata da Euclide nel fèllo lipo. Del di Banque D'Images

RM2AN424R–Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . : Come i trianoli ABC, & A C D, & i paradiogrammi E C, & dal parallélogrammo E C al Bparallélogrammo C F. I I. I Che qualfiuoglia triangolò fegato convna linea équidiftante à qualfiuoglialato , che i Iati dei famenegto fiano proporalitali . Venez che il triangolo ABC legato dalla li-nea D E equidillante alla B C, la proportio-ne dell A E alla E B Ga, venez dall A D alia D C :& quella è nota, eflendo la feconda propoita di-mollrata da Euclide nel fèllo lipo. Del di

Modo del Diere l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pratica . f)aralIeJogramo, nel qua-e rettilineo, fi collocaranno le linee diuecin guifa che lo com partii chino, e tuno e ttogruno, e duno, duno e duno e duno, duno, duno, duno, duno, duno, duno En due partivguali con la linea il, & da EFTO punto ! ìZlTflL cauifi la linea L M perpendiculairement alla Cap.drì a.HK. Dooi conitituifeafi la fuperri- Tratt0-eie HPON, libile alla fuperfìeie HIML, i.Tropojì-& vguale alli due parallélogrammi E>& F, per la terza propofitio- fio del s.ne del q Banque D'Images

RM2AN3C1G–Modo del Diere l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pratica . f)aralIeJogramo, nel qua-e rettilineo, fi collocaranno le linee diuecin guifa che lo com partii chino, e tuno e ttogruno, e duno, duno e duno e duno, duno, duno, duno, duno, duno, duno En due partivguali con la linea il, & da EFTO punto ! ìZlTflL cauifi la linea L M perpendiculairement alla Cap.drì a.HK. Dooi conitituifeafi la fuperri- Tratt0-eie HPON, libile alla fuperfìeie HIML, i.Tropojì-& vguale alli due parallélogrammi E>& F, per la terza propofitio- fio del s.ne del q

Modo del Dienstecar l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pratica . la cir-conferenza dell Alluui â′ Ã 5 (Ãpr²A le linee, che la legano, Venez riada A dans B da B da B in Qd en C^; Dj en C.D. Da min F; da M in G Dal INH; da K. in I, & finalmente da K in A,con la diligenza della mano tirando la linea tortuola, che palli per detti punti otteruati; cosÃ il dittegno (ara conclulo. Auertendo perÃ², che quanto piÃ¹ delleperpedicolari fi farano, che leghino la circonferenza di quel (ito,del quale(i vuoleleuare la pianta,tanto (i operaiapi Banque D'Images

RM2AN3N0M–Modo del Dienstecar l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pratica . la cir-conferenza dell Alluui â′ Ã 5 (Ãpr²A le linee, che la legano, Venez riada A dans B da B da B in Qd en C^; Dj en C.D. Da min F; da M in G Dal INH; da K. in I, & finalmente da K in A,con la diligenza della mano tirando la linea tortuola, che palli per detti punti otteruati; cosÃ il dittegno (ara conclulo. Auertendo perÃ², che quanto piÃ¹ delleperpedicolari fi farano, che leghino la circonferenza di quel (ito,del quale(i vuoleleuare la pianta,tanto (i operaiapi

Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . U--p. 6- SUlalIiMiòhèABCDckcondafe dalli tré conlefrti regolate AB, BC, CD, & dalla linea 4 A D par le prefflTe fi farà il parallélogrammo vgaafe al terreno eli effa,diuifò nelerre por-tioni EFG, faecóndo le propori delle fronti,& à faranco il retlineo IK. L fibile allo infcritto dell alluuione, il quale fi deuépoi compartire fecondo il fòlitomodo sfiammili fé langofo levguale ali angolo K,& la HI alla KL,& fé gli angoli IK,& le due li-nee HI Banque D'Images

RM2AN3705–Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . U--p. 6- SUlalIiMiòhèABCDckcondafe dalli tré conlefrti regolate AB, BC, CD, & dalla linea 4 A D par le prefflTe fi farà il parallélogrammo vgaafe al terreno eli effa,diuifò nelerre por-tioni EFG, faecóndo le propori delle fronti,& à faranco il retlineo IK. L fibile allo infcritto dell alluuione, il quale fi deuépoi compartire fecondo il fòlitomodo sfiammili fé langofo levguale ali angolo K,& la HI alla KL,& fé gli angoli IK,& le due li-nee HI

Modo del Suecar l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . li dui angoli F G H, H G K fono uguali à due retti,perche le due linee G F, G K fono tirare dans le Diuerfè parti dal puntoG della linea H G,& fono per drito per la «^.Dignità-, adùque li duiangoli G KI, IK L faranno ancre loro vguah à due retti, fendole due linee G K, Kl tirate per dritro dal punto K della lineaKI:& il medefimo lì dirà delli dui angoli EHG,GHI eflerevguali à due retti, & li due Hik, KIM parimente effere vg jahidueretti, douendo constilituite il paralle Banque D'Images

RM2AN46Y6–Modo del Suecar l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . li dui angoli F G H, H G K fono uguali à due retti,perche le due linee G F, G K fono tirare dans le Diuerfè parti dal puntoG della linea H G,& fono per drito per la «^.Dignità-, adùque li duiangoli G KI, IK L faranno ancre loro vguah à due retti, fendole due linee G K, Kl tirate per dritro dal punto K della lineaKI:& il medefimo lì dirà delli dui angoli EHG,GHI eflerevguali à due retti, & li due Hik, KIM parimente effere vg jahidueretti, douendo constilituite il paralle

Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . 3 R-. R F G L, Q Banque D'Images

RM2AN37E2–Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . 3 R-. R F G L, Q

Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . M N K. tra (la Come da 24 A 5 2-,II che fi fa,Come fi diflfe nella feconda del i$capo del terzo Trattatogli legnarà il punto C lontano dal D, per2 li.,che multiplicato poi con 5|-, farà 5-8 5 7 , & la radice qua-dra del prodotto (1 legniB lontanodal punto D ??> ma volendo ancho-ra trouare il pùtol, per il quale de-uepaflfare laltra linea diuidéte,che{èparà Titioda Caio, trouemoprima la quantità del triangoloAB a-, bifna pergölgneza Banque D'Images

RM2AN38W6–Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . M N K. tra (la Come da 24 A 5 2-,II che fi fa,Come fi diflfe nella feconda del i$capo del terzo Trattatogli legnarà il punto C lontano dal D, per2 li.,che multiplicato poi con 5|-, farà 5-8 5 7 , & la radice qua-dra del prodotto (1 legniB lontanodal punto D ??> ma volendo ancho-ra trouare il pùtol, per il quale de-uepaflfare laltra linea diuidéte,che{èparà Titioda Caio, trouemoprima la quantità del triangoloAB a-, bifna pergölgneza

Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . :-:^<<-:-^:-:-:-:0-ri^:-. ? Quelli del parallélogrammo, farà facile venire in cogitione dellaquantità di EFTO terreno dellalluione regolata. Hauendo già det-to nel 7 Cap. Del faecondo trattato-,che,hanendo noto i duo lati delparallélogrammo rettangoIo,fàrànota la quantità di eflb: Dunquefendo noti i lati dvno triangolo-, cioè, quegli, nolo e Turepertolo, a-, a-, a-, a-------------------------------------------------------- Banque D'Images

RM2AN3JH1–Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . :-:^<<-:-^:-:-:-:0-ri^:-. ? Quelli del parallélogrammo, farà facile venire in cogitione dellaquantità di EFTO terreno dellalluione regolata. Hauendo già det-to nel 7 Cap. Del faecondo trattato-,che,hanendo noto i duo lati delparallélogrammo rettangoIo,fàrànota la quantità di eflb: Dunquefendo noti i lati dvno triangolo-, cioè, quegli, nolo e Turepertolo, a-, a-, a-, a--------------------------------------------------------

Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . ? B eftrlfècojper il che tirado la linea *,dalli eftremi delli cófinati,paffaper il buó terreno-, Dopò regolili verlo il fiume AD,& DC: On-de.lè le fronti de deboranti, & quelle che riguardano il fiura-, (arano vrifnura, aprone, aprone, aprone, apruno, apruno, apruno, apruno, apralnui, apruno, apruno Ne Umilmente pollo:Attdo che ballaràdiuidere langolo ABC dans due parti vguali, oue-10 la linea A C, nel punto E, & iui porre lo {qua. Ad angolo Banque D'Images

RM2AN3DXX–Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . ? B eftrlfècojper il che tirado la linea *,dalli eftremi delli cófinati,paffaper il buó terreno-, Dopò regolili verlo il fiume AD,& DC: On-de.lè le fronti de deboranti, & quelle che riguardano il fiura-, (arano vrifnura, aprone, aprone, aprone, apruno, apruno, apruno, apruno, apralnui, apruno, apruno Ne Umilmente pollo:Attdo che ballaràdiuidere langolo ABC dans due parti vguali, oue-10 la linea A C, nel punto E, & iui porre lo {qua. Ad angolo

Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pratica . il ciò bicognaua. IO non poffo mancare di ponere anchora qui vn modo affai fa-cile pe-rcauarevna perpendiculairement, tratto dalla 3 1. Propofitionedel terzo dEuclide. SIA di nuouo la data retta linea AB,&che noi vogliamo cauare vna perpendiculaires-lare da vn punto dato in eifa, & fia per ho-ra nelleitremo A ?-, piglili il punto C fuoridella linea A B, acheté non conuenga coneffa B, & dans detto punto C pongali ilcompaffo,& fecondo linteruallo C A deferiuafì il cerchio E A D. Banque D'Images

RM2AN4A29–Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pratica . il ciò bicognaua. IO non poffo mancare di ponere anchora qui vn modo affai fa-cile pe-rcauarevna perpendiculairement, tratto dalla 3 1. Propofitionedel terzo dEuclide. SIA di nuouo la data retta linea AB,&che noi vogliamo cauare vna perpendiculaires-lare da vn punto dato in eifa, & fia per ho-ra nelleitremo A ?-, piglili il punto C fuoridella linea A B, acheté non conuenga coneffa B, & dans detto punto C pongali ilcompaffo,& fecondo linteruallo C A deferiuafì il cerchio E A D.

Modo del Dienstor l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pratica . unque da quello, & da molte altre à addutte dallo illsffo Euclide nel xiii. Liro, & da Tolomeo nel gt primo al-ni. • n°n ci è parlo di fbperchio di porla in quellaOpera: Oltra che riabbamo animo di moilrar forfè altrue,che la prefènte propofìtione fìa vtihfsima , &: Quali necefTiria in alcune forti di machine. La conlliturione di detta propoli-none farà mifla dei modo dEuclide, & di Tolomeo, & la dimo-ilratione à modo nollro. Banque D'Images

RM2AN41R2–Modo del Dienstor l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pratica . unque da quello, & da molte altre à addutte dallo illsffo Euclide nel xiii. Liro, & da Tolomeo nel gt primo al-ni. • n°n ci è parlo di fbperchio di porla in quellaOpera: Oltra che riabbamo animo di moilrar forfè altrue,che la prefènte propofìtione fìa vtihfsima , &: Quali necefTiria in alcune forti di machine. La conlliturione di detta propoli-none farà mifla dei modo dEuclide, & di Tolomeo, & la dimo-ilratione à modo nollro.

Modo del Dienstecar l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pratica . altre il Quadrato. Quelle, che moilrano comeshabbia a diuidere lAngolo, fonodi molta vtilità ,& maisimaimamente poiché in alcuni cafi la loia di-uizione dellAngolo renfloua fare folo la diuione delliuiuione ra-gioneuole, & ciunel, Capitafluo, Angiero, Angiero, Angiero, Angiero, Angiero, Angiero, Angiero, Angiero, Angiero, Angiero, Angiero, Angier À fin cheveniamo en cogitione del punto,oue debbia pafTare la linea diui-denteinfra due cantianti nella linea fondamentale,oc Bartolola giudic Banque D'Images

RM2AN4B1D–Modo del Dienstecar l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pratica . altre il Quadrato. Quelle, che moilrano comeshabbia a diuidere lAngolo, fonodi molta vtilità ,& maisimaimamente poiché in alcuni cafi la loia di-uizione dellAngolo renfloua fare folo la diuione delliuiuione ra-gioneuole, & ciunel, Capitafluo, Angiero, Angiero, Angiero, Angiero, Angiero, Angiero, Angiero, Angiero, Angiero, Angiero, Angiero, Angier À fin cheveniamo en cogitione del punto,oue debbia pafTare la linea diui-denteinfra due cantianti nella linea fondamentale,oc Bartolola giudic

Modo del Diere l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . ella compofìtione delle proper-tioni. Ma perche non palliamo cofa, la quale pretenda à tal co-gnitione, diremo prima, che colà fìa Anologia, ouero.fimilitudi-ne di due proportioni, la quale cauamo della 4. Diffinitione delquinto lib. DEuclide. I: ?• Quello, che fi a proporità , & difproporità. Écart. VII. R rroportionahta e vna limih-tudine di due ò più propor- Uulu * Come (aria per effempio, che la proportion della,quantità A,alla quantità B, forfè hmil Banque D'Images

RM2AN43D1–Modo del Diere l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . ella compofìtione delle proper-tioni. Ma perche non palliamo cofa, la quale pretenda à tal co-gnitione, diremo prima, che colà fìa Anologia, ouero.fimilitudi-ne di due proportioni, la quale cauamo della 4. Diffinitione delquinto lib. DEuclide. I: ?• Quello, che fi a proporità , & difproporità. Écart. VII. R rroportionahta e vna limih-tudine di due ò più propor- Uulu * Come (aria per effempio, che la proportion della,quantità A,alla quantità B, forfè hmil

Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . M B IH K O A Titio, et IDGHà Caio, viennent bi-iognaua. Hora, fi Come fi promTe, Ci è dimoftrato, che il vero mododcldmider Palluuioni è ilpropoitoda noi,& Cifono polli alcu-ni principij Geomerrici indrizzariallainrenone noltra : Habbia-mo poi rarrato delle proporrioni, & delle diuiiìo ni delle linee,& fìiperrìcie proporrionatamente, & dopoi alcuni principij, cheappararengono immédiatement aramenreaUalluuione -, dans oltre fi fono ad-dutri i calì,che ci fono parfi baileuoli : Banque D'Images

RM2AN2KH0–Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . M B IH K O A Titio, et IDGHà Caio, viennent bi-iognaua. Hora, fi Come fi promTe, Ci è dimoftrato, che il vero mododcldmider Palluuioni è ilpropoitoda noi,& Cifono polli alcu-ni principij Geomerrici indrizzariallainrenone noltra : Habbia-mo poi rarrato delle proporrioni, & delle diuiiìo ni delle linee,& fìiperrìcie proporrionatamente, & dopoi alcuni principij, cheappararengono immédiatement aramenreaUalluuione -, dans oltre fi fono ad-dutri i calì,che ci fono parfi baileuoli :

Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . Propofi. Lcap. A. Tratt,^Tratt. 1 r. Banque D'Images

RM2AN3GCP–Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . Propofi. Lcap. A. Tratt,^Tratt. 1 r.

Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . zi.Trop»fi,dcll.dEuc. PRIMA PROPOSTA. Da tre linee rette, che fiano vgualiàtre rette linee Dare, pofsiamo conili-tuire vn triangolo ; ma bigogna, chedue di quelle , prefe dans qual fi vogliamodo, fiano maggiori della rima-nente. Siano le tre linee dateA, B, C ?-, le quali fianoprefe due di quelle, inqual fi voglia modo,purche fiano maggiori del-la rimanente, cioè CHEV A, e B,fiano maggiori, che la C,& la A,& C,fiano maggiori,B,chorb, choi, choi, B, choroi Banque D'Images

RM2AN4983–Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . zi.Trop»fi,dcll.dEuc. PRIMA PROPOSTA. Da tre linee rette, che fiano vgualiàtre rette linee Dare, pofsiamo conili-tuire vn triangolo ; ma bigogna, chedue di quelle , prefe dans qual fi vogliamodo, fiano maggiori della rima-nente. Siano le tre linee dateA, B, C ?-, le quali fianoprefe due di quelle, inqual fi voglia modo,purche fiano maggiori del-la rimanente, cioè CHEV A, e B,fiano maggiori, che la C,& la A,& C,fiano maggiori,B,chorb, choi, choi, B, choroi

Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . EFGHI. notinfì le parti fudette del Cielo in lettere maggiori,Come L, P, S, M, in vna Croce ad angco RETRO : poi fi porrà dar principic a quella parte, che torna più còmodo al Topografo, & horaremo noi principio qui ha Oriente & Mezodinel puna, &inelfo punto porremo lo fquadro,&de li guardando per li traguardi,(in nel punto R legando coni raggi vifiui la circonferenza dellal-iuiuiuione nel puto B, & con legni, ouero palline faremo legnare !alinea retta ABR, & Banque D'Images

RM2AN3NTJ–Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . EFGHI. notinfì le parti fudette del Cielo in lettere maggiori,Come L, P, S, M, in vna Croce ad angco RETRO : poi fi porrà dar principic a quella parte, che torna più còmodo al Topografo, & horaremo noi principio qui ha Oriente & Mezodinel puna, &inelfo punto porremo lo fquadro,&de li guardando per li traguardi,(in nel punto R legando coni raggi vifiui la circonferenza dellal-iuiuiuione nel puto B, & con legni, ouero palline faremo legnare !alinea retta ABR, &

RM2AN2TJ8–Modo del Alligvioni da qvello di Bartolo, Et de gli agrimensori diversoMostrato con ragioni mathématiche & con pratica . lo delli tre cr)nfinanti,per il ino do deHantecedente,ie ben la fronte AB regolata è minore della fronte BregoIara,peril chepropióga- remo meil de imo/HI punnel to Lintieo, linikle, linikl Che diuidono le pornoni f vna dallaltra faranno la O QJ>, N M, di maniera, che la fuperfìcie HIAQ^P farà vguale alla portione E, & la fu pei fide OQJPMNK. Vguale alla portione F -, & il triangolo M N Lguellio de lingualdo, G. fec

Modo del Diplero da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pratica . o Euclide.Onde la linea A B non fegata è fegata dans le parti A F, F G, & G B,lilili parti A E, D D C della linea A C, Come fi richiedeua.Dalla précède propofitione Ci cauadi potier legare in dueparti vna linea retta fafecondo vna data propore. * K C III Pofsiamo fegare vna linea retta in dueparti fafecondo vna data propore. Siala data retta linea AB, e la propor-tione Come quella della D alla C , bifò-rnb legare Là B nelle due parti,fècondo laproport Banque D'Images

RM2AN4165–Modo del Diplero da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pratica . o Euclide.Onde la linea A B non fegata è fegata dans le parti A F, F G, & G B,lilili parti A E, D D C della linea A C, Come fi richiedeua.Dalla précède propofitione Ci cauadi potier legare in dueparti vna linea retta fafecondo vna data propore. * K C III Pofsiamo fegare vna linea retta in dueparti fafecondo vna data propore. Siala data retta linea AB, e la propor-tione Come quella della D alla C , bifò-rnb legare Là B nelle due parti,fècondo laproport

Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . Che DELLE ALLVVIONI. 35 I I. Che fi polla propiongare vna linea ret-ta, terminata en continuo , e dritta-mente . Venez è la linea retta B C, fi pofTa propiongare ; ò dalla parteverfo A,ouero verfo D, dans conti- 1^ C nuo, e dirittamente. /ÌT- D I I.. Che.da qual fi voglia centro con qual fi voglia in-teruallo, fi polla deferi-nere vn cerchio . Proclo, faecondo Gemino, dés, che ragioneuofe cofaè collo-Care queiti tre principij fra le dimande ; sì per la facilitation, sì pe Banque D'Images

RM2AN4BWE–Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . Che DELLE ALLVVIONI. 35 I I. Che fi polla propiongare vna linea ret-ta, terminata en continuo , e dritta-mente . Venez è la linea retta B C, fi pofTa propiongare ; ò dalla parteverfo A,ouero verfo D, dans conti- 1^ C nuo, e dirittamente. /ÌT- D I I.. Che.da qual fi voglia centro con qual fi voglia in-teruallo, fi polla deferi-nere vn cerchio . Proclo, faecondo Gemino, dés, che ragioneuofe cofaè collo-Care queiti tre principij fra le dimande ; sì per la facilitation, sì pe

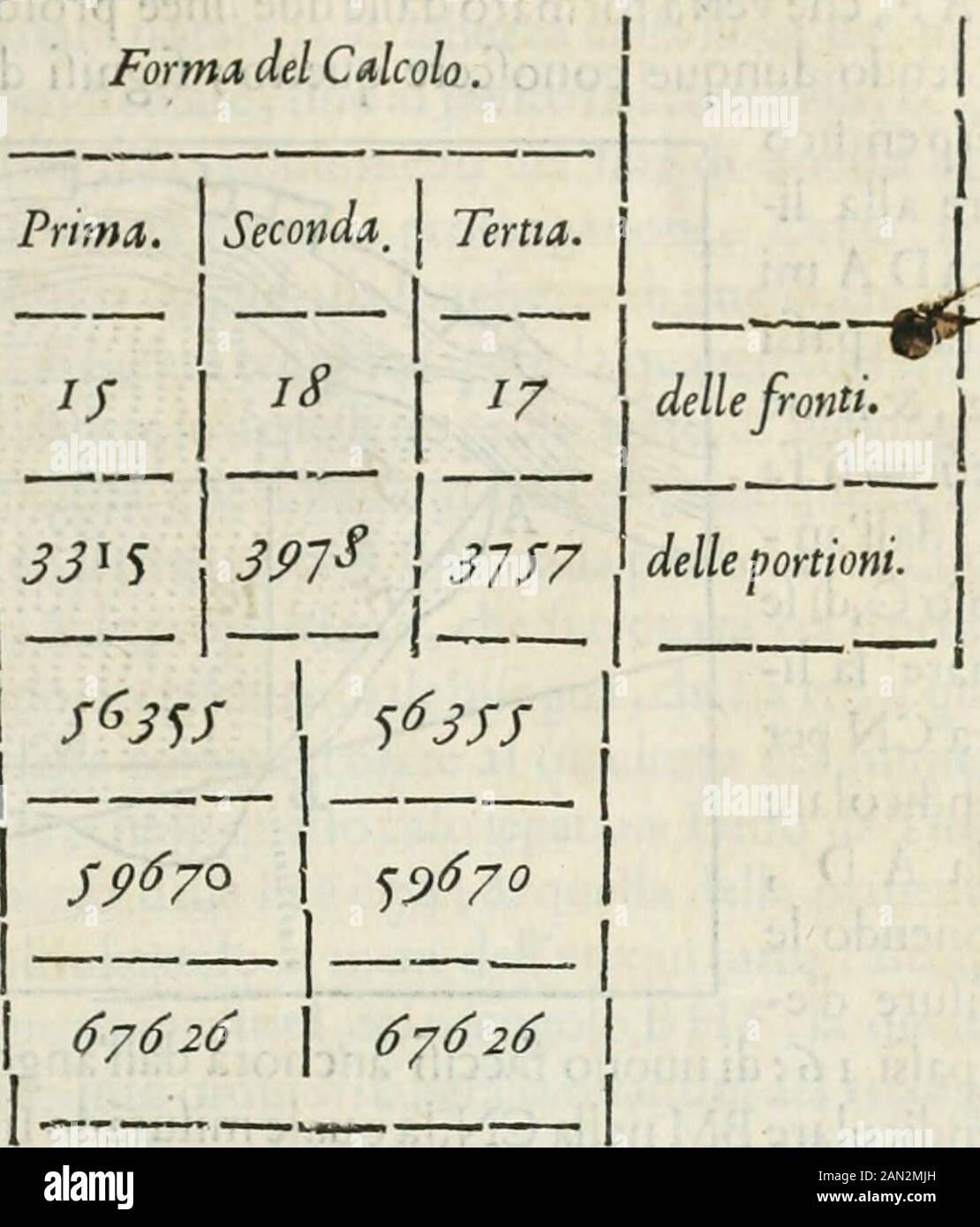Modo del Dienstleistóra da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pratica . if prima DELLE ALLVVIONI. II>? Forma del Calcolo. Prima. Seconda l Primo ordine. ! // Secondo ordine. 33 LS. Prima del faecondo Ordine nella 17, terza del primo Ordine-, & fémulriplicaremo 18,feconda del primo Ordine con 3515VI pro-durrò 5.9670 (ara vguale à quello , che fi farà mulriplicando3978, faonda del faecondo Orcon 15-, Finalmente, 616, 616-3, 616-3 (ara vgua-le a quel lo, che fi farà mulriplicando 18 con 3 Banque D'Images

RM2AN2MJH–Modo del Dienstleistóra da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pratica . if prima DELLE ALLVVIONI. II>? Forma del Calcolo. Prima. Seconda l Primo ordine. ! // Secondo ordine. 33 LS. Prima del faecondo Ordine nella 17, terza del primo Ordine-, & fémulriplicaremo 18,feconda del primo Ordine con 3515VI pro-durrò 5.9670 (ara vguale à quello , che fi farà mulriplicando3978, faonda del faecondo Orcon 15-, Finalmente, 616, 616-3, 616-3 (ara vgua-le a quel lo, che fi farà mulriplicando 18 con 3

Modo del Aldere l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pratica . uale Alla B,&Lac A è dimoiata vguale Alla B.Adunque lvna, e laltra di efleC A, &CB fono veguali AB: Onde le,tre linee A B, A C, BC faranno vguali fid loro:Adunque il Triangolo A B C è equilatero : Et è conitiruita (opala linea A B terminata, Come fi richiedeua. Si hi da fapeie,che fopra la data retta linea terminata, fé le puòanchora conftiruire il triangolo Ifòcelo, & lo Scaleno, Come fi ve-de à Proclo, & dans moli altri moderni. I I. Davn punto dato pof Banque D'Images

RM2AN4AK3–Modo del Aldere l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pratica . uale Alla B,&Lac A è dimoiata vguale Alla B.Adunque lvna, e laltra di efleC A, &CB fono veguali AB: Onde le,tre linee A B, A C, BC faranno vguali fid loro:Adunque il Triangolo A B C è equilatero : Et è conitiruita (opala linea A B terminata, Come fi richiedeua. Si hi da fapeie,che fopra la data retta linea terminata, fé le puòanchora conftiruire il triangolo Ifòcelo, & lo Scaleno, Come fi ve-de à Proclo, & dans moli altri moderni. I I. Davn punto dato pof

Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . 11. Tropo-fittone deli.dEuclide, DELLE ALLVVrONf. 47. fiamo tirare vna linea retta perpen-dicolare . SIA la data retta lineainfinita A B,il dato pun-to C,che non è in e(Tà>bi-fogna tirare vna linea retta perpendiculairement, piglia-li dellaltra parte della li-nea B, qual (1 vogliapD, & dal centro con Cintertil, C, A delcriuafì Nelli due punti E, & F, poi par la prima propofìtionedi quello capo legali la linea E F Banque D'Images

RM2AN49FC–Modo del Dienstère l'allvvioni da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pritica . 11. Tropo-fittone deli.dEuclide, DELLE ALLVVrONf. 47. fiamo tirare vna linea retta perpen-dicolare . SIA la data retta lineainfinita A B,il dato pun-to C,che non è in e(Tà>bi-fogna tirare vna linea retta perpendiculairement, piglia-li dellaltra parte della li-nea B, qual (1 vogliapD, & dal centro con Cintertil, C, A delcriuafì Nelli due punti E, & F, poi par la prima propofìtionedi quello capo legali la linea E F

Modo del Dienstódica da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pratica . sì facile ladandone-, per-che bigognarà fare il paralle-logrammo EF vguale al ter-reno di detalluudiui Co-deporondo, hefeci & poiformare il retilinio IK L M, fibile al regolato della alluuio-ne , & umilmente porto, & an-ello congiungere gli punti I&L conia linea il, fìmile alla $onde per collocare la linea chiùdente dal punto M, fuciali CA-dere la linea M,perpendiculairement,fradella sont Banque D'Images

RM2AN3DFB–Modo del Dienstódica da qvello di Bartolo, et de gli agrimensori diversoMostrato con ragioni mathématiche & con pratica . sì facile ladandone-, per-che bigognarà fare il paralle-logrammo EF vguale al ter-reno di detalluudiui Co-deporondo, hefeci & poiformare il retilinio IK L M, fibile al regolato della alluuio-ne , & umilmente porto, & an-ello congiungere gli punti I&L conia linea il, fìmile alla $onde per collocare la linea chiùdente dal punto M, fuciali CA-dere la linea M,perpendiculairement,fradella sont

Livressur objet Photos Stock & Des Images

Livressur objet Photos Stock & Des Images

Confirmation de téléchargement

Confirmation du mot de passe

Résultats de la recherche pour Livressur objet les photos et les images (807)

Filtrer par collections d’agences

Développeur de recherches

Profitez de superbes fonctionnalités avec votre compte gratuit

Inspirez-vous pour votre prochain projet !